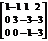Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные системы уравнений. Основные определения. Матричная запись.Линейной системой уравнений наз-ся система вида: Матрица, составленная из коэффициентов системы, наз-ся основной матрицей системы. Матрица вида: А̃= Вводят столбцы:
Используя введённые обозначения, линейную систему (1) можно записать в т. н. матричном виде: A∙X=H (2) Матричное равенство (2) равносильно системе (1) согласно правилам умножения матриц. Упорядоченное множество чисел С1, С2, …, Сn наз-ся решением системы (1), если после подстановки этих чисел уравнение системы вместо неизвестных х1, х2, …, хn каждое из уравнений системы превращается в верное равенство. Столбец решений:
Если линейная система ур-ий имеет одно единственное решение, эта система наз-ся определенной. Если система имеет не одно решение, то неопределенной. Если не имеет решений, то наз. несовместной. Если имеет хотя бы одно решение, то совместной. Две системы, имеющие одинак. множ-ва решений (т. е. когда каждое решение одной из них является решением другой), наз. равносильными, или эквивалентными. => 2 несовместные системы эквивалентны. Элементарные преобразования над системой: 1) умножение любого ур-я на любое число, отличное от 0. 2) прибавление к обеим частям одного из ур-й системы обеих частей другого ур-ния, умноженных на любое число. 3) перемена мест ур-й системы. Очевидно, что элементарные преобразования над системой соответствуют элементарным преобразованиям над строками её расширенной матрицы. Очевидно, что в результате элементарных преобразований над системой получается система, равносильная исходной. Формулы Крамера  Рассмотрим линейную систему из n уравнений относительно n неизвестных:
Основная матрица этой системы будет квадратной. Ее определитель Систему можно записать в матричном виде: A∙X=H (4). Если определитель ∆=detA≠0, то система наз-ся невырожденной. В этом случае основная матрица системы имеет обратную А-1, кот. может быть найдена по формуле:
Умножим обе части матричного равенства (4) слева на матрицу А-1; получим А-1АХ= А-1Н, учитывая, что А-1А=Е, ЕХ= А-1Н, а т. к. ЕХ=Х, то имеем Х= А-1Н (5). Это равенство даст решение системы (3) в матричной форме. Перепишем равенство (5) в развернутом виде Отсюда, по правилу умножения матриц, имеем В скобках правой части стоит сумма произведения чисел h1,h2,…,hn на алгебраические дополнения j-столбца матрицы А. Согласно теореме замещения, это выражение = определителю кот. получается из определителя ∆ заменой в нем j-того столбца на столбец из свободных членов
Эти формулы наз-ся формулами Крамера, где ∆-определитель системы, ∆j-определитель, который получается из определителя системы заменой в нем j-того столбца на столбец из свободных членов. Таким образом, мы показали, что любая невырожденная система из n уравнений относительно n неизвестных имеет единственное решение, которое может быть найдено по формулам Крамера.
Метод Гаусса (Метод последовательного исключения неизвестных) Этот метод рассмотрим на примере невырожденной системы 3х уравнений из 3х неизвестных
1. Прямой ход метода Гаусса. 1) Записываем расширенную матрицу, соответствующую этой системе
2) При помощи преобразований эквивалентности, приводим эту матрицу к так называемой трапециевидной форме. => 2. Обратный ход метода Гаусса. Записываем линейную систему, соответствующую новой расширенной матрице. Эта система будет равносильна исходной.
из системы: х3=3, подставим во 2е уравнение: 3х2=3-3∙3=6, х2= 2, подставим х2 и х3 в 1е уравнение: х1-2+3=2, х1=1. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 491. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) называется расширенной матрицей системы.
называется расширенной матрицей системы.

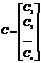
 наз. определителем системы.
наз. определителем системы.

 , где (j=1,2, …,n).
, где (j=1,2, …,n). (6)
(6)
 =>
=> =>
=>