
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача двух тел. Приведенная массаРассмотрим задачу о движении двух взаимодействующих только между собой материальных точек. Вследствие однородности и изотропности пространства потенциальная энергия взаимодействия может зависеть только от расстояния между точками. Функция Лагранжа для данной задачи запишется в форме Рассматриваемая система материальных точек замкнута. Поэтому ее импульс сохраняется, и система отсчета центра инерции является инерциальной системой отсчета. Задачу будем решать в системе отсчета центра инерции. Начало координат поместим в центр инерции, что дает
Введем радиус-вектор
С помощью формул (4.2) и (4.3) выразим векторы
Потенциальная энергия теперь зависит только от величины вектора
Выраженная через радиус-вектор Функция Лагранжа (4.6) — это функция Лагранжа одной материальной точки массы
Масса  Если масса одной материальной точки, например Поскольку масса Солнца намного больше массы каждой из планет Солнечной системы, то в первом приближении можно пренебречь взаимодействием планет между собой и движением Солнца вокруг центра инерции Солнечной системы. В этом приближении движение отдельной планеты рассматривается как движение материальной точки в поле тяготения Солнца. Учет взаимодействия планет между собой приводит к задаче многих тел, взаимодействующих между собой. Эта задача не может быть сведена к квадратурам и решается приближенными методами.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 709. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.1)
(4.1) (4.2)
(4.2)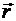 , направленный от первой материальной точки ко второй:
, направленный от первой материальной точки ко второй: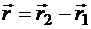 (4.3)
(4.3) и
и  через вектор
через вектор  ;
;  (4.4)
(4.4) и
и  через вектор
через вектор  , кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной материальной точки массой
, кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной материальной точки массой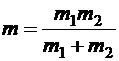 (4.5)
(4.5)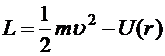 (4.6)
(4.6)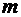 , движущейся в потенциальном поле, зависящем только от расстояния до начала координат. Такое потенциальное поле называется центральным полем. Сила, действующая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля:
, движущейся в потенциальном поле, зависящем только от расстояния до начала координат. Такое потенциальное поле называется центральным полем. Сила, действующая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля: (4.7)
(4.7) , много больше массы другой материальной точки, то из формул (4.4) и (4.5) получим, что приближенно
, много больше массы другой материальной точки, то из формул (4.4) и (4.5) получим, что приближенно  ,
,  ,
,  , то есть центр инерции системы двух тел совпадает с более массивным телом, а приведенная масса равна массе менее массивного тела. В этом случае задача двух тел сводится к задаче о движении одного тела в потенциальном поле, создаваемом другим телом.
, то есть центр инерции системы двух тел совпадает с более массивным телом, а приведенная масса равна массе менее массивного тела. В этом случае задача двух тел сводится к задаче о движении одного тела в потенциальном поле, создаваемом другим телом.