
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вынужденные одномерные колебанияЧасто механические системы, совершающие малые колебания, подвергаются воздействию внешней вынуждающей силы, зависящей от времени. Пусть потенциальная энергия одномерной системы в поле вынуждающей силы равна
где введено обозначение
При подстановке ее в уравнение (5.7) получим уравнение вынужденных колебаний Уравнение (5.23) — это уже неоднородное дифференциальное уравнение. Его решение дается суммой общего решения однородного уравнения (5.10) и частного решения уравнения (5.23): Наиболее интересным случаем вынужденных колебаний является случай, когда внешняя обобщенная сила представляет собой гармоническую функцию где
В правой части уравнения (5.26) стоит экспонента. Поэтому его частное решение
Представим постоянную
Тогда действительная часть общего решения уравнения(5.23) с гармонической вынуждающей силой (5.25) запишется в виде  В отсутствие трения
Фаза вынужденных колебаний совпадает с фазой вынуждающей силы. Амплитуда вынужденных колебаний растет при Уравнение малых колебаний в случае резонанса принимает вид
При резонансе фаза вынужденных колебаний на Рассмотрим поведение системы вблизи резонанса, когда частота вынуждающей силы мало отличается от частоты свободных колебаний. Положим, что В выражении (5.33) нужно учитывать только действительную часть, которая равна
Уравнение (5.34) можно интерпретировать как уравнение колебаний с часютой Если Перейдем к общему случаю, когда присутствует трение
При резонансе, как и в отсутствие трения, колебания отстают от вынуждающей силы на
то есть чем выше добротность, тем меньше полуширина
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 566. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
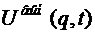 . Разложим ее в ряд вблизи положения равновесия, ограничиваясь приближением первого порядка
. Разложим ее в ряд вблизи положения равновесия, ограничиваясь приближением первого порядка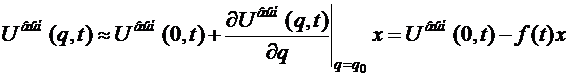 (5.21)
(5.21)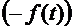 для производной от потенциальной энергии по координате, вычисленной в положении равновесия. Слагаемое
для производной от потенциальной энергии по координате, вычисленной в положении равновесия. Слагаемое 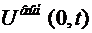 не зависит от обобщенных координат и обобщенных скоростей и поэтому не дает вклада в уравнения Лагранжа. Отбросим его и запишем функцию Лагранжа механической системы, находящейся в поле внешней вынуждающей силы:
не зависит от обобщенных координат и обобщенных скоростей и поэтому не дает вклада в уравнения Лагранжа. Отбросим его и запишем функцию Лагранжа механической системы, находящейся в поле внешней вынуждающей силы: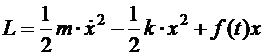 (5.22)
(5.22)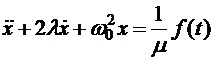 (5.23)
(5.23)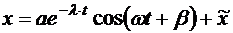 (5.24)
(5.24)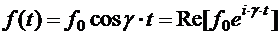 (5.25)
(5.25)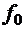 — действительная постоянная. Для гармонической вынуждающей силы уравнение (5.23) удобно записать и решать в комплексной форме:
— действительная постоянная. Для гармонической вынуждающей силы уравнение (5.23) удобно записать и решать в комплексной форме: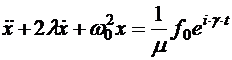 (5.26)
(5.26)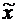 также ищем в форме экспоненты
также ищем в форме экспоненты 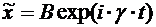 . Подставляя
. Подставляя 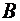 :
: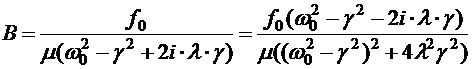 (5.27)
(5.27)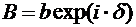 , где
, где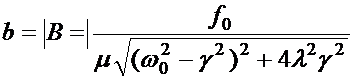 ;
; 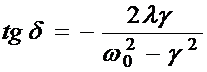 (5.28)
(5.28)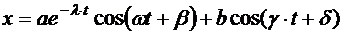 (5.29)
(5.29)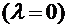 вынужденные колебания (5.29) являются суммой свободных колебаний с частотой
вынужденные колебания (5.29) являются суммой свободных колебаний с частотой 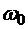 и вынужденных колебаний с частотой вынуждающей силы
и вынужденных колебаний с частотой вынуждающей силы 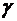 и амплитудой, зависящей от частоты:
и амплитудой, зависящей от частоты: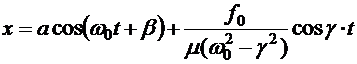 (5.30)
(5.30)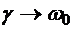 . Если
. Если 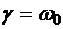 , то наступает резонанс и решение (5.30) не имеет смысла. В этом случае частное решение уравнения (5.26) необходимо искать в виде
, то наступает резонанс и решение (5.30) не имеет смысла. В этом случае частное решение уравнения (5.26) необходимо искать в виде 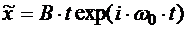 Для постоянной
Для постоянной 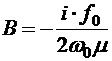 (5.31)
(5.31)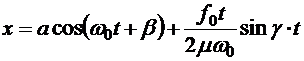 *. (5.32)
*. (5.32)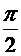 отличается от фазы вынуждающей силы. Амплитуда вынужденных колебаний монотонно растет с течением времени, и колебания быстро перестают быть малыми.
отличается от фазы вынуждающей силы. Амплитуда вынужденных колебаний монотонно растет с течением времени, и колебания быстро перестают быть малыми.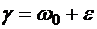 , где
, где 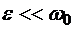 . Выражение (5.30), записанное в комплексной форме, можно привести к виду
. Выражение (5.30), записанное в комплексной форме, можно привести к виду 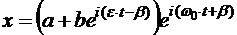 (5.33)
(5.33)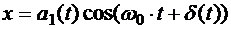 , (5.34) где
, (5.34) где 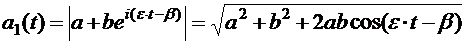 (5.35)
(5.35) 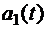 и начальная фаза
и начальная фаза 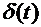 которых медленно меняются с частотой
которых медленно меняются с частотой 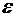 . Как видно из (5.35), амплитуда заключена в пределах
. Как видно из (5.35), амплитуда заключена в пределах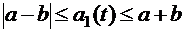 (5.36)
(5.36) и
и  близки друг к другу, то временами колебания будут почти прекращаться, а после опять возобновляться. Такое поведение системы называют биениями.
близки друг к другу, то временами колебания будут почти прекращаться, а после опять возобновляться. Такое поведение системы называют биениями.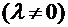 При наличии трения первое слагаемое в (5.29) быстро обращается в нуль за счет экспоненциального множителя. В установившемся режиме остается только второе слагаемое. Вынужденные колебания происходят с частотой вынуждающей силы, но отстают от нее по фазе. Начальная фаза вынужденных колебаний, как видно из (5.27) и (5.28), лежит в пределах
При наличии трения первое слагаемое в (5.29) быстро обращается в нуль за счет экспоненциального множителя. В установившемся режиме остается только второе слагаемое. Вынужденные колебания происходят с частотой вынуждающей силы, но отстают от нее по фазе. Начальная фаза вынужденных колебаний, как видно из (5.27) и (5.28), лежит в пределах 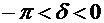 . При сильном трении, когда
. При сильном трении, когда 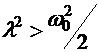 , амплитуда вынужденных колебаний монотонно убывает с ростом частоты вынуждающей силы. Если трение мало, то амплитуда максимальна при резонансной частоте
, амплитуда вынужденных колебаний монотонно убывает с ростом частоты вынуждающей силы. Если трение мало, то амплитуда максимальна при резонансной частоте 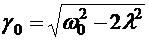 .
. Рассмотрим отдельно случай, когда трение очень мало:
Рассмотрим отдельно случай, когда трение очень мало: 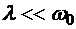 . Тогда в первом приближении по
. Тогда в первом приближении по 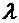 резонансная частота
резонансная частота 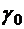 совпадает с частотой
совпадает с частотой 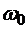 . Вблизи резонанса положим
. Вблизи резонанса положим 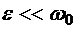 . В первом приближении по
. В первом приближении по 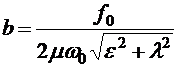 ;
; 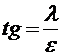 (5.37)
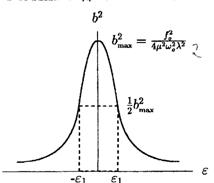
(5.37) 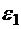 частоту, для которой квадрат амплитуды уменьшается в два раза, то находим, что
частоту, для которой квадрат амплитуды уменьшается в два раза, то находим, что 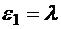 . Для характеристики систем, совершающих вынужденные колебания, вводится понятие добротности. Добротность — это отношение максимальной амплитуды для резонансной частоты к амплитуде, отвечающей близкой к нулю частоте вынуждающей силы. Используя выражение (5.28) для амплитуды и считая
. Для характеристики систем, совершающих вынужденные колебания, вводится понятие добротности. Добротность — это отношение максимальной амплитуды для резонансной частоты к амплитуде, отвечающей близкой к нулю частоте вынуждающей силы. Используя выражение (5.28) для амплитуды и считая 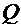 значение:
значение: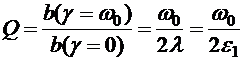 (5.38)
(5.38)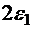 резонансной кривой и тем выше поднимается ее пик.
резонансной кривой и тем выше поднимается ее пик.