
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Связь фундаментальных законов сохранения с симметриями пространства и времениКак уже отмечалось, пространство в классической механике постулируется однородным и изотропным, а время — однородным. С этими свойствами симметрии пространства и времени в лагранжевом формализме связывают существование фундаментальных законов сохранения энергии, импульса и момента импульса для замкнутой системы материальных точек. Под замкнутой системой материальных точек понимается система, на которую не только не действуют внешние силы, но и в которой не происходит превращения механической энергии в другие виды энергии, например, в тепловую энергию или в энергию электромагнитного поля. Для замкнутой механической системы вследствие однородности времени все моменты времени одинаковы. Поэтому функция Лагранжа не должна явно зависеть от времени. В предыдущем параграфе было показано, что если функция Лагранжа не зависит явно от времени, то механическая энергия сохраняется, то есть из однородности времени следует закон сохранения энергии для замкнутой механической системы. / Равенство (3.38) дает полную производную от обобщенной энергии по времени Если функция Лагранжа не зависит явно oт времени, то правая часть в формуле (3.40) равна нулю и обобщенная энергия сохраняется при движении механической системы. / Вследствие однородности пространства для замкнутой механической системы все точки пространства равноправны. Поэтому ее функция Лагранжа не должна зависеть от положения механической системы в пространстве. Она может зависеть только от относительных расстояний между материальными точками системы. Положение механической системы как целого в пространстве можно задать с помощью координат ее центра инерции. Если выбрать обобщенные координаты так, чтобы три из них были координатами центра инерции механической системы, то вследствие однородности пространства эти координаты будут циклическими. Обозначая координаты центра инерции как X,Y,Z, запишем согласно связи обобщенного импульса с импульсами отдельных материальных точек механической системы:  сопряженные им сохраняющиеся обобщенные импульсы:
При смещении центра инерции координаты всех точек получают одинаковые приращения. Например, при смещении центра инерции вдоль оси ОХ на
Обобщенный импульс Закон сохранения момента импульса замкнутой системы материальных точек в лагранжевом формализме выводится из изотропности пространства. Вследствие изотропности пространства ориентация механической системы относительно пространства не должна влиять на ее механические свойства. Пусть одна из обобщенных координат выбрана так, что ее изменение приводит к повоpoтy всей механической системы вокруг некоторой оси на угол В некоторых случаях отдельные фундаментальные законы сохранения выполняются для систем материальных точек, взаимодействующих с другими телами. Если внешнее поле обладает некоторыми свойствами симметрии, то им соответствуют законы сохранения. Например, в центрально симметричном поле сохраняется момент импульса механической системы, определенный относительно центра симметрии поля Это следует из того, что повороты механической системы относительно оси, проходящей через центр симметрии поля, не влияют на движение механической системы.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 615. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
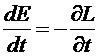 (3.40)
(3.40) (3-31)
(3-31) ;
;  ;
;  (3.44)
(3.44) получим
получим  , и, следовательно,
, и, следовательно, ;
;  (3.45)
(3.45) равен проекции импульса системы материальных точек на ось ОХ. Аналогичные выводы можно сделать относительно обобщенных импульсов
равен проекции импульса системы материальных точек на ось ОХ. Аналогичные выводы можно сделать относительно обобщенных импульсов 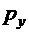 и
и  , то есть для замкнутой системы материальных точек сохраняются все три проекции импульса, и, следовательно, вектор импульса
, то есть для замкнутой системы материальных точек сохраняются все три проекции импульса, и, следовательно, вектор импульса  замкнутой системы материальных точек остается постоянным.
замкнутой системы материальных точек остается постоянным. . Так как механическая система не может реагировать на ориентацию в изотропном пространстве, то координата
. Так как механическая система не может реагировать на ориентацию в изотропном пространстве, то координата