
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Получение уравнений Лагранжа из принципа Гамильтона.Из принципа Гамильтона обычным методом вариационного исчисления можно получить дифференциальные уравнения. Наряду с зависимостью
Это уже было отмечено ранее, что дифференцирование по времени и варьирование можно переставлять. Вариации координат рассматриваются такими, что в моменты времени Действие для пробных функций Интеграл от одного из слагаемых первой суммы в (3.5) вычислим по частям: Согласно условию (3.4), на пределах интегрирования
Поскольку вариации координат  Несмотря на то, что функция Лагранжа равна разности кинетической и потенциальной энергии, в выборе функции Лагранжа имеется некоторый произвол. Две функции Лагранжа, отличающиеся на полную производную по времени от произвольной функции координат и времени, дают одни и те же уравнения движения. Покажем это. Пусть Тогда для разности действий, отвечающих этим функциям Лагранжа, получим: Вследствие того, что вариация координат на пределах интегрирования Ур-ия Лагранжа обобщаются на механические системы, в которых действуют непотенциальные силы. Выражение для; обо6щенной непотенциалыюй силы нужно добавить в правую часть уравнений Лагранжа. Они тогда принимают вид В частном случае, когда непотенциальные силы являются силами трения, пропорциональными первой степени скорости, они могyт быть получены из диссипативной функции Рэлея:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 559. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , описывающей истинное движение механической системы, рассмотрим пробные функции
, описывающей истинное движение механической системы, рассмотрим пробные функции  , отличающиеся от
, отличающиеся от  (3.1) Дифференцируя равенство (3.1) по времени, найдем
(3.1) Дифференцируя равенство (3.1) по времени, найдем  (3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:
(3.2) Откуда следует, что вариация скорости равна производной от вариации координаты:  . (3.3).
. (3.3). и
и 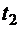 . они равны нулю:
. они равны нулю:  (3.4)
(3.4) разложим в ряд в линейном приближении по
разложим в ряд в линейном приближении по  , и
, и  :
:  (3.5)
(3.5) (3.6)
(3.6) . Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим
. Поэтому первое слагаемое в последнем равенстве обращается в нуль. Подставляя теперь результат из (3.6) в (3.5) и записывая вариацию действия, получим (3.7)
(3.7) . В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа:
. В результате получается система дифференциальных уравнений, которые в механике называются уравнениями Лагранжа:  (3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат
(3.8) Уравнения Лагранжа - это система дифференциальных уравнений относительно неизвестных обобщенных координат  и
и  отличаются на полную производную по времени от некоторой функции
отличаются на полную производную по времени от некоторой функции  ;
;  (3.9)
(3.9)
 и
и  равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями
равны. Поэтому онибудут обращаться в нуль одними и теми же зависимостями  , где
, где  (3,10)
(3,10)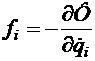 ;
; 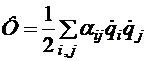 (3.11) Коэффициенты
(3.11) Коэффициенты  могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид
могут зависеть от координат и характеризуют силы трения в механической системе. Для механических систем, в которых силы трения могут быть описаны диссипативной функцией Рэлея, уравнения Лагранжа имеют вид  (3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда
(3.12) Ур-ия (3.10) и (3.12) не могут быть получены на основе вариационного принципа. Они выводятся непосредственно из принципа Даламбера. В лагранжевом формализме можно включать в уравнения движения силы немеханической природы. Например, ур-ия движения заряда 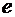 в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:
в электромагнитном поле получаются из фунции Лагранжа, которая содержит слагаемые, описывающие взаимодействие заряда с полем:  (3.13) где
(3.13) где  и
и 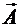 — скалярный и векторный потенциалы электромагнитного поля,
— скалярный и векторный потенциалы электромагнитного поля, 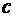 — скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности.
— скорость света в вакууме. Электромагнитные величины записаны в гауссовой системе единиц. При замене функции Лагранжа классической механики на функцию Лагранжа специальной теории относительности ур-ия Лагранжа дают ур-ия движения механики спец. теории относительности.