
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Энергия, з-н изменения кинетической энергии с-мы материальных точек.Закон 2 Ньютона. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. Второй закон Ньютона связывает ускорение тела с действующей на него силой:
Так как масса — величина постоянная, то уравнение (1.1) можно записать в форме
Если уравнение второго закона Ньютона (11) умножить скалярно на
Величина называется кинетической энергией материальной точки, а произведение то эта функция называется потенциалъной энергией. В этом случае из уравнения (1.9) вытекает закон сохранения механической энергии, равной сумме потенциальной и кинетической энергии: Силы, для которых выполняется условие (1,10), называются потенциальными силами. Проекции потенциальной силы на оси координат выражаются через частные производные от потенциальной энергии:
Несколько тел, каждое из которых можно рассматривать как материальную точку, составляют систему материальных точек. Для каждой материальной точки можно записать уравнение второго закона Ньютона
В уравнении (1.13) индексы  Из уравнений (1.13) вытекают несколько важных законов. Если просуммируем их по всем материальным точкам системы, то получим
Записывая уравнения изменения кинетической энергии (1.9) для всех материальных точек системы и суммируя их по всем материальным точкам, получим
где Потенциальная энергия зависит от координат всех материальных точек. Силу, действующую на материальную точку с номером а, можно найти по формулам
где производные берутся по координатам материальной точки 4. С-ма отсчета центра инерции. Преобразование импульса, момента импульса, энергии…. Пусть имеется система отсчета, которая движется поступательно со скоростью Всегда можно найти систему отсчета, в которой импульс системы материальных точек равен нулю. Эта система отсчета движется со скоростью центра инерции системы материальных точек и называется системой отсчета центра инерции. Из (1.23) видно, что импульс системы отсчета записывается через скорость центра инерции и массу системы материальных точек так же, как импульс одной материальной точки: масса которой равна массе системы материальных точек и скорость которой равна скорости центра инерции. Закон изменения импульса системы материальных точек (1.16) тогда запишется как второй закона Ньютона для материальной точки:
Преобразование кинетической энергии при переходе в систему отсчета центра инерции. Подставляя закон сложения скоростей (1.22) в выражение для кинетической энергии системы, получим Т.к. в системе отсчета центра инерции импульс системы материальных точек =0, то последнее слагаемое пропадает и мы имеем Кинетическая энергия системы материальных точек равна сумме кинетической энергии движения системы со скоростью центра инерции и кинетической энергии
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 774. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.1)
(1.1) (1.6)
(1.6) и учесть, что
и учесть, что  , то можно получить соотношение
, то можно получить соотношение (1.9)
(1.9)
 — работой силы на перемещении
— работой силы на перемещении 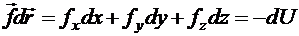 (1.10)
(1.10) (1.11)
(1.11) ;
;  ;
;  ; (1.12)
; (1.12)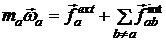 (1.13)
(1.13) дают номер материальной точки. Действующие на материальную точку силы разделены на внешние
дают номер материальной точки. Действующие на материальную точку силы разделены на внешние  и внутренние
и внутренние  . Внешние силы — это силы, действующие со стороны тел, не входящих в систему материальных точек. Внутренние силы — это силы, действующие на материальную точку со стороны других тел, составляющих систему материальных точек. Здесь
. Внешние силы — это силы, действующие со стороны тел, не входящих в систему материальных точек. Внутренние силы — это силы, действующие на материальную точку со стороны других тел, составляющих систему материальных точек. Здесь  — сила, действующая на материальную точку, индекс которой
— сила, действующая на материальную точку, индекс которой  , со стороны материальной точки с номером
, со стороны материальной точки с номером  .
. (1.14) ,
(1.14) , (1.19)
(1.19)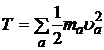 — кинетическая энергия системы материальных точек. В формуле (1.19) работа внутренних сил не обращается в пуль. Если сумма работ внешних и внутренних сил является полным дифференциалом, то из уравнения (1.19) вытекает закон сохранения полной механической энергии
— кинетическая энергия системы материальных точек. В формуле (1.19) работа внутренних сил не обращается в пуль. Если сумма работ внешних и внутренних сил является полным дифференциалом, то из уравнения (1.19) вытекает закон сохранения полной механической энергии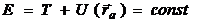 (1.20)
(1.20)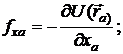

 (1.21)
(1.21)  относительно неподвижной системы отсчета. Скорость
относительно неподвижной системы отсчета. Скорость  (1.22) Подставляя (1.22) в формулу для импульса системы материальных точек (
(1.22) Подставляя (1.22) в формулу для импульса системы материальных точек (  ) получим:
) получим:  (1.23) Можно найти такую систему отсчета, в которой импульс системы материальных точек
(1.23) Можно найти такую систему отсчета, в которой импульс системы материальных точек  =0. Про такую систему отсчета естественно сказать, что это система отсчета, в которой система материальных точек как целое покоится. Это вовсе не означает, что скорости всех материальных точек равны нулю. Полагая в формуле (1.23)
=0. Про такую систему отсчета естественно сказать, что это система отсчета, в которой система материальных точек как целое покоится. Это вовсе не означает, что скорости всех материальных точек равны нулю. Полагая в формуле (1.23)  (1.24) Из соотношения (1.24) видно, что эта скорость может быть выражена как производная от следующего радиуса-вектора;
(1.24) Из соотношения (1.24) видно, что эта скорость может быть выражена как производная от следующего радиуса-вектора;  . (1.25) Радиус-вектор
. (1.25) Радиус-вектор  указывает на точку, которая называется центром инерции системы материальных точек. Из определения центра инерции видно, что он совпадает с центром масс системы материальных точек.
указывает на точку, которая называется центром инерции системы материальных точек. Из определения центра инерции видно, что он совпадает с центром масс системы материальных точек. , (1.26)
, (1.26) (1.27) Центр инерции системы материальных точек движется как материальная точка, масса которой равна массе системы материальных точек и к которой приложена сила, равная сумме действующих на систему материальных точек внешних сил. В частности, если сумма внешних сил =0, то центр инерции движется равномерно и прямолинейно, и система отсчета центра инерции является инерциальной системой отсчета.
(1.27) Центр инерции системы материальных точек движется как материальная точка, масса которой равна массе системы материальных точек и к которой приложена сила, равная сумме действующих на систему материальных точек внешних сил. В частности, если сумма внешних сил =0, то центр инерции движется равномерно и прямолинейно, и система отсчета центра инерции является инерциальной системой отсчета.
 (1.28)
(1.28)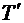 внутреннего движения материальных точек в системе отсчета центра инерции. Так как потенциальная энергия не зависит от системы отсчета, то аналогичное разбиение на внутреннюю энергию и энергию движения системы как целого будет справедливо для полной механической энергии:
внутреннего движения материальных точек в системе отсчета центра инерции. Так как потенциальная энергия не зависит от системы отсчета, то аналогичное разбиение на внутреннюю энергию и энергию движения системы как целого будет справедливо для полной механической энергии:  (1.29) В системе отсчета центра инерции момент импульса не зависит от выбора начала координат. Покажем это. Пусть начала координат смещено из точки
(1.29) В системе отсчета центра инерции момент импульса не зависит от выбора начала координат. Покажем это. Пусть начала координат смещено из точки  в точку
в точку 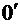 , как показано на рис. 1.1. Тогда радиусы-векторы материальной точки
, как показано на рис. 1.1. Тогда радиусы-векторы материальной точки  относительно двух начал координат связаны равенством
относительно двух начал координат связаны равенством  (1.30) Подставляя это выражение для
(1.30) Подставляя это выражение для  в определение момента импульса системы материальных точек (
в определение момента импульса системы материальных точек (  (1.18)), получим
(1.18)), получим  (1.31) Здесь
(1.31) Здесь  — момент импульса системы материальных точек относительно нового начала координат. Так как в системе отсчета центра инерции импульс системы материальных точек
— момент импульса системы материальных точек относительно нового начала координат. Так как в системе отсчета центра инерции импульс системы материальных точек  равен нулю, то второе слагаемое в (1.31) обращается в нуль и.
равен нулю, то второе слагаемое в (1.31) обращается в нуль и.  . Преобразование момента импульса системы материальных точек при переходе в систему отсчета центра инерции. Пусть в некоторый момент времени начала координат двух систем отсчета совпадают. Тогда
. Преобразование момента импульса системы материальных точек при переходе в систему отсчета центра инерции. Пусть в некоторый момент времени начала координат двух систем отсчета совпадают. Тогда  . Скорости материальных точек относительно двух систем отсчета связаны соотношением (1.22). Подставляя (1.22) в определение момента импульса (1.18) и учитывая, что движущаяся система отсчета — это система отсчета инерции, получим
. Скорости материальных точек относительно двух систем отсчета связаны соотношением (1.22). Подставляя (1.22) в определение момента импульса (1.18) и учитывая, что движущаяся система отсчета — это система отсчета инерции, получим  . (1.32) Т.к. в системе отсчета центра инерции
. (1.32) Т.к. в системе отсчета центра инерции