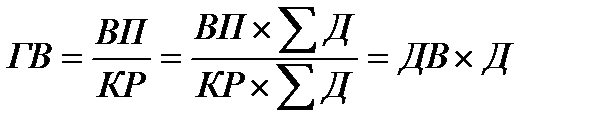ДЕТЕРМИРОВАННОЕ МОДЕЛИРОВАНИЕ.ТИПЫ ФАКТОРНЫХ МОДЕЛЕЙ.

Сущность моделирования заключается в том, что взаимосвязь между показателями передается в форме математического уравнения (модели). В соответствии с типом факторного анализа различают детерминированные (функциональные) и стохастические (корреляционные) модели. При детерминированном моделировании необходимо соблюдать следующие требования:1. факторы и сама модель должны реально существовать;2. показатели, входящие в модель, должны находиться в причинно-следственной связи;3. все показатели модели должны иметь источники информации и единицы измерения;4. модель должна обеспечивать возможность измерения влияния каждого фактора. При этом сумма влияния всех факторов должна равняться общему изменению результативного показателя. Это суть проверочной строки или балансовой увязки.

Моделирование мультипликативных факторных систем осуществляется путем разложения факторов исходной модели на факторы-сомножители. Исходная двухфакторная мультипликативную модель: ВП=СОС*ФО. В свою очередь, по второму порядку модель будут иметь следующий вид: ФО=УДА*ФОА Подставив факторы второго порядка в исходную зависимость, получим трехфакторную мультипликативную модель: ВП=СОС*УДА *ФОА. Аналогичным образом осуществляется моделирование аддитивных факторных систем, то есть за счет расчленения факторов исходной модели на их элементы.

К классу кратных моделей применяют следующие способы их преобразования:1. способ удлинения — удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Исходная модель:

2. способ формального разложения — удлинение знаменателя исходной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Исходная модель:

3. способ расширения — развитие модели путем умножения числителя и знаменателя исходной модели на один или несколько новых показателей.

4. способ сокращения — создание новой модели путем деления числителя и знаменателя исходной модели на один и тот же показатель. Например,