
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бесконечно большие последовательности и их свойстваБесконечно малым последовательностям в некотором смысле противопоставляются бесконечно большие последовательности(или простобесконечно большие). Определение. Последовательность {yn} называется бесконечно большой, если ее значения yn по абсолютной величине становятся и остаются бóльшими сколь угодно большóго наперед заданного числа l >0, начиная с некоторого номера nl, зависящего от l: |yn| > l, лишь только п > nl. Как и в случае, бесконечно малой, здесь также следует подчеркнуть, что конкретные значения yn бесконечно большой последовательности {yn} способны сделаться бóльшими произвольно взятого большóго числа l лишь в процессе своего изменения. Из приведенного определения следует, что последовательность бесконечно большая, если в любой конечной l-окрестности нуля (-l,l) содержится конечное число членов последовательности и вне этой окрестности ее членов бесконечно много. Заметим, что бесконечно большая последовательность является неограниченной, но обратное утверждение несправедливо, так как не всякая неограниченная последовательность является бесконечно большой. Например, последовательность, значения которой заданы формулой Примерами бесконечно больших могут служить последовательности: Между бесконечно большими и бесконечно малыми последовательностями существует простая связь, которая устанавливается следующими теоремами:  1. Если последовательность {yn} с отличными от нуля членами является бесконечно большой, то последовательность 2. Если последовательность {хn} с отличными от нуля членами является бесконечно малой, то последовательность Эти теоремы примем без доказательства. Если последовательность {yn} является бесконечно большой, то говорят также, что она имеет предел ∞ или стремится к ∞, и пишут
Когда значение lim yn = +∞, Из приведенных выше примеров бесконечно больших последовательностей, очевидно, последовательность Таким образом, к «несобственным числам» +∞ и -∞, с которыми мы уже сталкивались, мы здесь присоединили еще ∞, без знака; следует помнить, что их применение имеет совершенно условный смысл, и остерегаться производить над этими «числами» арифметические операции. Введение бесконечных пределов не нарушает теоремы 1 (п.5.2) о единственности предела, а теоремы 3 и 4 (п.5.2) легко распространяются и на случай бесконечных пределов (из них теорема 4 – лишь в предположении, что речь идет о бесконечности определенного знака).
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 654. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , не ограничена. Действительно, для любого l > 0 найдутся такие ее члены, которые удовлетворят неравенству
, не ограничена. Действительно, для любого l > 0 найдутся такие ее члены, которые удовлетворят неравенству  Но нельзя подобрать такое натуральное число nl, чтобы " n > nl выполнялось то же неравенство
Но нельзя подобрать такое натуральное число nl, чтобы " n > nl выполнялось то же неравенство 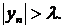
 Эти последовательности пробегают значения натуральных чисел, но первая со знаком плюс, вторая со знаком минус, третья же – с чередующимися знаками.
Эти последовательности пробегают значения натуральных чисел, но первая со знаком плюс, вторая со знаком минус, третья же – с чередующимися знаками. будет бесконечно малой.
будет бесконечно малой. будет бесконечно большой.
будет бесконечно большой. ∞,
∞,  ∞,
∞,  ∞.
∞. бесконечно большой последовательности {yn} (по крайней мере, для достаточно больших n) сохраняют определенный знак (плюс или минус); тогда, в соответствии со знаком, говорят, что последовательность {yn} имеет предел +∞ или - ∞ и пишут
бесконечно большой последовательности {yn} (по крайней мере, для достаточно больших n) сохраняют определенный знак (плюс или минус); тогда, в соответствии со знаком, говорят, что последовательность {yn} имеет предел +∞ или - ∞ и пишут стремится к +∞, последовательность
стремится к +∞, последовательность  стремится к -∞. Что же касается третьей последовательности
стремится к -∞. Что же касается третьей последовательности  то она, как и все бесконечно большие последовательности, стремится к ∞, но про нее нельзя сказать, что она стремится к +∞, или, что она стремится к -∞.
то она, как и все бесконечно большие последовательности, стремится к ∞, но про нее нельзя сказать, что она стремится к +∞, или, что она стремится к -∞.