
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Арифметические операции над последовательностями, имеющими пределТеорема 1(о пределе суммы (разности)).Если последовательности {yn} и {хn} имеют конечные пределы: lim yn =
Доказательство. Из условия теоремы следует, что yn = a + un, xn = b + vn, где последовательности {un} и {vn} – бесконечно малые. Тогда yn ± xn = (a ± b) + + (un ± vn). Здесь последовательности {un ± vn} есть бесконечно малые по теореме 1 (п.5.3); следовательно, пользуясь вторым определением предела, можно утверждать, что последовательности {yn ± xn} имеют пределы, равные a ± b, что и требовалось доказать. Эта теорема и ее доказательство переносятся на случай любого конечного числа слагаемых. Теорема 2 (о пределе произведения). Если последовательности {yn} и {хn} имеют конечные пределы: lim yn = Доказательство аналогично доказательству теоремы 1. Теорема обобщается на случай конечного числа сомножителей. Следствие.Постоянный множитель можно выносить за знак предела: lim lyn = l lim yn , где l - постоянное число. Действительно, если последовательность постоянная Теорема 3(о пределе частного). Если последовательности {yn} и {хn} имеют конечные пределы: lim yn =
Доказательство. Из условий yn®a и xn®b имеем yn = a + un и xn = b + vn, где последовательности {un} и {vn} – бесконечно малые. Тогда
По свойствам бесконечно малых последовательность 
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 597. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
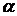 , lim хn = b, то и последовательности {yn ± xn} также имеют конечный предел, причем
, lim хn = b, то и последовательности {yn ± xn} также имеют конечный предел, причем .
. = {l}, то ее предел lim хn = l. Тогда по теореме 2: lim {yn · xn} = lim yn·lim хn=l lim yn.
= {l}, то ее предел lim хn = l. Тогда по теореме 2: lim {yn · xn} = lim yn·lim хn=l lim yn.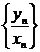 также имеет конечный предел, а именно
также имеет конечный предел, а именно .
. .
. есть бесконечно малая. Тогда и последовательность
есть бесконечно малая. Тогда и последовательность 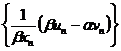 также бесконечно малая, как произведение ограниченной последовательности
также бесконечно малая, как произведение ограниченной последовательности  на бесконечно малую. Таким образом, по второму определению предела следует, что
на бесконечно малую. Таким образом, по второму определению предела следует, что  или
или  .
.