
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бесконечно малые последовательности и их свойстваОпределение 1. Последовательность {yn}, имеющая своим пределом нуль, называется бесконечно малой последовательностью или просто бесконечно малой. Если в определении предела последовательности положить a = 0, то неравенство (1.8) примет вид |yn – 0| = |yn| < e (для n > ne). Таким образом, данное выше определение бесконечно малой последовательности можно сформулировать и без упоминания термина ²предел². Определение 2.Последовательность {yn} называется бесконечно малой, если ее значения yn по абсолютной величине становятся и остаются меньшими сколь угодно наперед заданного числа e >0, начиная с некоторого номера ne , зависящего от e : |yn| < e , лишь только n > ne . В дальнейших теоремах нам придется рассматривать одновременно две (или больше) последовательности, сочетая их между собой знаками арифметических действий. При этом знаки относятся к соответствующим значениям последовательностей. Говоря, например, о сумме двух последовательностей {xn} и {yn}, которые принимают соответствующие значения x1, x2, x3,...,xn, и y1, y2, y3,...,yn будем иметь в виду последовательность {xn + yn}, принимающую последовательность значений x1 + y1,…, xn + yn , … Теорема 1. Сумма (разность) конечного числа бесконечно малых последовательностей есть также последовательность бесконечно малая. Доказательство теоремы опускаем. Теорема 2. Последовательность {xn × mn}, представляющая собой произведение ограниченной последовательности {xn} на бесконечно малую последовательность {mn}, есть последовательность бесконечно малая. Доказательство.Пусть для всех значений n |xn| < b,где b > 0. Если задано произвольное число  Следствие. Произведение бесконечно малой последовательности на последовательность, имеющую конечный предел, есть последовательность бесконечно малая. Действительно, так как последовательность имеет конечный предел, то она ограничена и тем самым выполнены условия теоремы. Теорема 3. Для того чтобы последовательность {yn} имела своим пределом постоянное число a, необходимо и достаточно, чтобы существовала такая бесконечно малая последовательность {xn}, что yn = a + xn . (1.9) Доказательство.Необходимость. Пусть последовательность {yn} имеет предел Обозначим yn – a = xn. Тогда " n > ne |xn| < e, т.е. lim xn = 0. Следовательно, последовательность {xn} бесконечно малая. Таким образом, lim yn = Достаточность. Пусть последовательность {yn} представлена в виде (1.9), где lim xn = 0. Это означает, что Теперь окончательно заключаем: lim yn = a Условие (1.9) можно прочитать так: любой член сходящейся последовательности равен сумме предела последовательности и соответствующего члена бесконечно малой последовательности. Замечание. Если для бесконечно малой последовательности {xn} использовать второе из приведенных выше определений без упоминания термина "предел", то теорема 3 позволяет дать для понятия "предел" другое определение (равносильное старому). Определение 3. Постоянное число a называется пределом последовательности {yn}, если существует такая бесконечно малая последовательность {xn}, что yn = a + xn. Примеры. 1. Рассмотрим последовательности, общие члены которых заданы формулами: Все три последовательности представляют собой бесконечно малые, т.е. имеют пределом нуль. Действительно, для них Отметим, что значения первой последовательности все время больше своего предела 0, второй - все время меньше его, третьей же – попеременно становятся то больше, то меньше его. 2. Важный пример бесконечно малой дает последовательность {yn} = {qn}, где |q| < 1. Для доказательства того, что yn ® 0, рассмотрим неравенство |yn| = |q|n < e ; оно равносильно таким: n lg|q| < lg e или Знак неравенства изменен на обратный, так как lg|q| < 0. Таким образом, если положить (считая e < 1) ne Замечание.Тот факт, что последовательность {yn} - бесконечно малая, не означает (еcли она не нуль), что в отдельности взятое значение yn этой последовательности может квалифицироваться как «малое» число. Например, бесконечно малая последовательность {yn} с общим членом |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 659. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 > 0, то по числу
> 0, то по числу 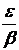 для бесконечно малой {mn} найдется такой номер ne , что для n > ne будет |mn| <
для бесконечно малой {mn} найдется такой номер ne , что для n > ne будет |mn| < 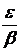 . Тогда для тех же значений n очевидно, |xn × mn| = |xn| × |mn| < b
. Тогда для тех же значений n очевидно, |xn × mn| = |xn| × |mn| < b 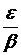 =
= 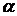 . Это означает, что для любого
. Это означает, что для любого 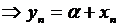 , где {xn} - бесконечно малая последовательность.
, где {xn} - бесконечно малая последовательность.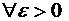 $ ne , что " n > ne выполняется неравенство |xn| < e. Из равенства (1.9) xn = yn – a. Тогда " n > ne справедливо неравенство |yn -
$ ne , что " n > ne выполняется неравенство |xn| < e. Из равенства (1.9) xn = yn – a. Тогда " n > ne справедливо неравенство |yn - 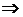 lim yn = a.
lim yn = a. yn = a + xn.
yn = a + xn.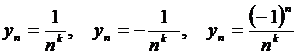 , где k – любое положительное число, т.е.
, где k – любое положительное число, т.е. 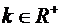 .
.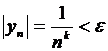 , лишь только
, лишь только 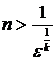 . Таким образом, в качестве ne можно взять, например, наибольшее целое число, содержащееся в
. Таким образом, в качестве ne можно взять, например, наибольшее целое число, содержащееся в  ,т.е. E
,т.е. E  .
.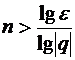 .
.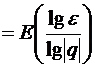 , то упомянутое неравенство выполняется и, следовательно, yn ® 0.
, то упомянутое неравенство выполняется и, следовательно, yn ® 0.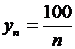 при п = 1 имеет значение y1 = 100, которое, естественно, не может рассматриваться как «малое» число, близкое к точке «ноль» на числовой оси.
при п = 1 имеет значение y1 = 100, которое, естественно, не может рассматриваться как «малое» число, близкое к точке «ноль» на числовой оси.