ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение и геометрическое истолкование предела последовательности

Пусть задана числовая последовательность {y_n}, где y_n – значения числовой функции f, переменного nÎN; т.е. y_n = f(n) или y_n = f_n ,а f : N®R.

Определение. Постоянное число a называется пределом числовой последовательности {y_n}, если для каждого положительного числа e, сколь бы мало оно ни было, найдется такое натуральное число n_e ,зависящее от e, что все члены последовательности с номерами n > n_e ,удовлетворяют неравенству

| y_n - a | < e.                                                   (1.8)

Тот факт, что a является пределом последовательности {y_n}, записывают так:  или .

Геометрически определение предела последовательности можно истолковать следующим образом.

Неравенство (1.8), как мы знаем, равносильно следующим: -e < y_n - a < e  или a - e < y_n  < a + e. Изобразим числа a, a ± e и значения y_n последовательности точками на числовой оси y (рис.12).

Точка a будет пределом последовательности {y_n}, если существует такое n_e , что все члены y_n последовательности, начиная с n > n_e , окажутся в                 e -окрестности точки a, т.е. какую бы ни взяли малую e - окрестность точки a, если внутри этой окрестности окажется бесконечное множество членов последовательности (с n > n_e ), а вне ее разве лишь конечное число (не более n_e первых членов), то эта точка будет пределом последовательности.

Рис. 12

Если последовательность {y_n} имеет конечный предел a, то ее называют сходящейся и говорят, что эта последовательность сходится к a или стремится к a, и пишут:  y_n ® a.

Постоянная последовательность {y_n} = {a} имеет пределом число a и является сходящейся последовательностью.

Пример: Доказать, что последовательность с общим членом  имеет предел, равный единице.

Доказательство. Рассмотрим разность  и оценим ее абсолютную величину: . Выражение 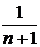 меньше любого числа e > 0, если . Этим и доказано, что y_n®1. Действительно, выберем , тогда " n > n_e ; получаем, что |y_n – 1| < e, откуда, по определению, lim y_n = 1.