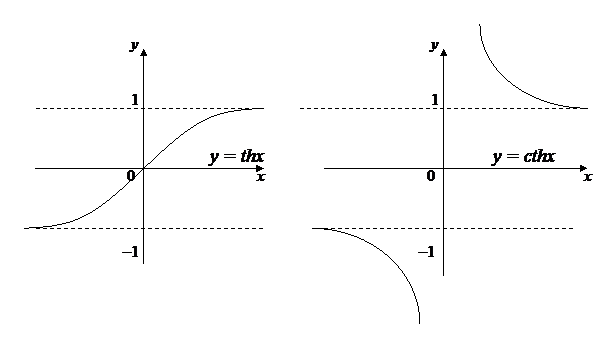ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ

Основные (простейшие) элементарные функции

К основным элементарным функциям относятся следующие, аналитическим способом, заданные функции.

1. Показательная функция: у = а^х и обратная ей логарифмическая функция: у = log_a x, где а – положительное число не равное единице. Графики этих функций показаны на рис.2.

2. Степенная функция: y = х^a, где aÎR. Если a = n – натуральное число, функция определена в бесконечном интервале (-∞, +∞) рис.3 и 4, если же a целоеотрицательное число: a = –n , то функция y = х ^–n = 1/хⁿ определена при всех значениях х, кроме х = 0. График такой функции показан на рис.10. При a дробном, мы имеем здесь радикал. Например, пусть a = 1/n и ; эта функция обратная для y = хⁿ и определена для всех значений х если n – нечетное, и лишь для неотрицательных значений – при n четном (рис.3 и 4).

Наконец, если a – иррациональное число, мы будем предполагать, что x > 0 и значение y определять путем логарифмирования и потенцирования:    ln y = a ln x,отсюда y = e^{a ln x}.

3. Тригонометрические функции: y = sin x; y = cos x; y = tg x; y = ctg x и обратные тригонометрические функции: y = arcsin x; y = arcos x; y = arctg x; y = arcctg x.

Рис. 10

Основные элементарные функции служат базой для образования широкого класса функций, которые называются элементарными.

Элементарные функции

К элементарным функциям относятся функции, образованные из основных элементарных функций и чисел посредством четырех арифметических действий и их композиций (сложные функции) последовательно примененных конечное число раз. Например:

 и т.п.

Существуют и не элементарные функции. К ним относятся, например, функции y = E(x) – “целая часть x” (см. гл.1,§2, п.2.1), функция Дирихле, которая определяется так:

и функция “сигнум х”, которая обозначается через signx:

К алгебраическим элементарным функциям относятся:

1. Целая рациональная функция (многочлен)

                              (1.6)

где  и х – действительные числа, n – натуральное число.

Эта функция образована из основной элементарной функции у = x^a,где aÎN, и чисел  путем сложения и умножения. Естественная область применения: бесконечный интервал (– ∞, +∞);

2. Дробно – рациональная функция, которая представлена в виде отношения двух целых рациональных функций относительно x

                                         .               (1.7)

Областью определения дробно – рациональной функции (речь идет о естественной области применения) является множество всех действительных чисел кроме тех, для которых знаменатель обращается в нуль;

3. Иррациональная функция. Это функция, в которой, кроме указанных выше действий, применяется еще и операция извлечения корня, т.е. в основной элементарной функции y = x^a a может принимать не только целые, но и дробные значения. Область применимости такого выражения устанавливается для каждого конкретного случая отдельно (см., например, гл.1, § 2, п.2.3).

Все прочие элементарные функции (показательные, логарифмические, тригонометрические и др.) относятся к трансцендентным. В качестве примера рассмотрим гиперболические функции. Так называются функции вида

                                      ;

;      

(гиперболический синус, косинус, тангенс, котангенс); они определены для всех значений x,исключая сth x,который теряет смысл при x = 0.

Эти функции проявляют аналогию с тригонометрическими функциями.

Так, имеют место формулы (обратить внимание на знаки):

сh (x ± y) = ch x ch y ± sh x sh y,

sh (x ± y) = sh x ch y ± ch x sh y,

из которых при y = x, в частности, следует:

ch²x – sh²x = 1;   ch 2x = ch²x + sh²x;     sh 2x = 2 sh x ch x.

Графики гиперболических функций изображены на рис.11.

Рис. 11 (Переделать, асимптоты)

Ограниченные функции

Определение. Функция f(x), определенная на множестве P, называется ограниченной сверху или снизу, если множество ее значений f(P) является ограниченным множеством соответственно сверху или снизу.

Если f(P)является ограниченным (или неограниченным) множеством, то говорят, что функция f(x) ограничена (или неограничена).

Основные элементарные функции f(x) = xⁿ, n – четное натуральное число и y(x) = a^x, определенные на множестве R действительных чисел(P = R),относятся к функциям, ограниченных снизу. Для обеих функций точные нижние границы одинаковы, т.е. inf f(R) = inf y(R) = 0. Для множества f(R) точная нижняя граница принадлежит этому множеству, а для множества y(R) – нет.

Функции f(x) = sin x, j(x) = cos x, y(x) = arcsin x, g(x) = arcos x, h(x) = arctg x и u(x) = arcctg x ограничены: inf f(R) = inf j(R) = –1;

inf y([– 1,1]) = inf h(R) = –p/2; inf g([– 1,1]) = inf u(R) = 0;

sup f(R) = supj(R) = 1; supy([– 1,1]) = sup h(R) = p/2; sup g([– 1,1]) = sup u(R) = p.

Остальные основные элементарные функции f(x) = xⁿ, n – нечетное натуральное число, j(x) = log_ax, y(x) = tg x и g(x) = ctg x неограничены.

Монотонные функции

Определение. Если для двух любых различных значений аргумента x₁и x₂, взятых из области определения Р функции f, из неравенства x₁< x₂ следует, что

а) f(x₁) < f(x₂),то функция f называется возрастающей в области Р,

б) f(x₁) £ f(x₂),то функция f называется неубывающей в области Р,

в) f(x₁) > f(x₂),то функция f называется убывающей в области Р,

г) f(x₁)³ f(x₂),то функция f называется невозрастающей в области Р.

Функции всех этих типов носят общее название монотонных.

Из основных элементарных функций монотонными на всей области их существования являются следующие функции: f(x) = xⁿ, n – нечетное натуральное число (возрастающая); y = a^x (возрастающая, если a > 1, убывающая, если 0 < a < 1); y = log_a x (возрастающая, если a > 1, убывающая, если 0 < a < 1); y = arcsin x (возрастающая); y = arccos x (убывающая); y = arctg x (возрастающая); y = arсctg x (убывающая).

Остальные основные элементарные функции монотонными являются лишь на некоторых подмножествах, выделенных из всей области существования соответствующей функции. Например, функция y = sin x на всей числовой оси не является монотонной. Однако на отдельно выделенных отрезках                            [–p/2+kp,p/2+kp], где kÎZ, данная функция является монотонной. На отрезках, для которых k = 0, ±2, ±4, ... функция y = sinx является возрастающей, а на отрезках, для которых k = ±1, ±3, ±5, ... – убывающей.

Четные и нечетные функции

Определение. Пусть функция f(x) определена в конечной (–a,a) или бесконечной (–∞, +∞) окрестности точки нуль, кроме, может быть, самой точки нуль. Если при противоположных по знаку значениях аргумента, взятых из данной окрестности, значения функции равны между собой, то функция называется четной: f(–x) = f(x).

Если же при аналогичных условиях значения функции противоположны по знаку f(–x) = – f(x),то функция называется нечетной.

Основные элементарные функции: y = xⁿ, где n – четное натуральное число; y = cos x – четные.

Функции y = sin x, y = xⁿ, где n – нечетное натуральное число; y = tgx; y = ctg x; y = arcsin x; y = arcctg x – нечетные.

Функции y = a^x, y = log_ax, y = arccos x, y = arcctgx не являются ни четными, ни нечетными.

График четной функции симметричен относительно оси Oy, график нечетной – относительно начала координат.

Периодические функции

Определение. Функция f(x) называется периодической, если существует такое наименьшее положительное число T ¹0, что при любых значениях аргумента x, взятых из области определения функции выполняется равенство: f(x) = f(x+kT), где k – любое целое число. Число T называется периодом функции.

Из основных элементарных функций периодическими являются следующие функции: y = sin x, T = 2p; y = cosx, T = 2p; y = tgx, T = p; y = ctgx, T = p.