
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Некоторые теоремы о последовательностях, имеющих пределТеорема 1.Если последовательность имеет предел, то этот предел единственный. Доказательство. Допустим противное. Пусть последовательность {yn} имеет два предела lim yn = a и lim yn = b, где a ¹ b, для определенности возьмем a < b. Выберем e > 0 так, чтобы Следствие. Если две последовательности {xn} и {yn} при всех их изменениях равны: xn = yn, причем каждая из них имеет конечный предел: lim xn = a,lim yn = b, то равны и эти пределы: a = b. Теорема 2. Если последовательность {yn} имеет конечный предел a, то она ограничена, в том смысле, что все ее значения составляют ограниченное множество. Доказательство. Так как lim yn = a, то в любую e-окрестность точки a попадают все yn, за исключением разве лишь конечного числа точек yn. Пусть начиная с n = ne+1 все Выберем из чисел a - e и a +e наибольшее по модулю m = max (|a - e|,|a +e|). Тогда | yn| < m¢ " n > ne . Теперь для конечного множества чисел |y1|,|y2|,|y3|,...., Заметим, что обратное утверждение не выполняется, так как не всякая ограниченная последовательность имеет предел. Например, последовательность  Теорему 2 дополним леммой, доказательство которой аналогично доказательству теоремы 2. Лемма. Если последовательность {yn}, у которой yn ¹ 0 " nÎN имеет предел, отличный от нуля, то последовательность Справедлива следующая теорема, которую примем без доказательства. Теорема 3.Если для последовательностей {xn} и {yn}, имеющих конечные пределы a и b, и, начиная с некоторого номера, для всех последующих членов выполняются неравенства xn ³ yn илиxn > yn, то lim xn ³lim yn или a ³ b. Следует обратить внимание на то, что из строгого неравенства xn > yn , вообще говоря, не вытекает строгое же неравенство lim xn > lim yn ,а только по-прежнему lim xn ³ lim yn. Так, например, Замечание. Знак > всюду может быть заменен знаком < . Теорема 4.(Гурьева о трех последовательностях). Если для трех последовательностей {xn}, {yn}, {zn}, начиная с некоторого номера, выполняются неравенства xn ≤ yn ≤ zn , причем последовательности {xn} и {zn} стремятся к общему пределу a: lim xn = lim zn = a, то и последовательность {yn} имеет тот же предел: lim yn= a.. Доказательство. Зададимся произвольным e > 0. Поэтому e, прежде всего, найдется такой номер n1, что при n > n1 a - e < xn < a +e. Затем найдется такой номер n2, что при n > n2 a - e < zn< a +e. Пусть ne будет больше обоих чисел n1и n2; тогда при n > ne выполняются оба предшествующих двойных неравенств и поэтому a - e < xn ≤ yn ≤ zn < a +e . Окончательно, при n > ne a - e < yn < a +e или | yn - a | < e . Это означает, что lim yn = a .
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 630. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Поскольку yn®a, то найдется такой номер n1, что для n > n1 будет выполняться неравенство a - e < yn < a +e. С другой стороны, раз yn ® b, то найдется такой номер n2,что для n > n2 окажется b - e < yn < b +e. Если взять номер n большим и n1, и n2, то соответствующие значения yn последовательности {yn} будут одновременно принадлежать двум интервалам (a - e,a +e) и (b - e,b +e), которые не пересекаются, т.е. (a - e,a +e) ∩ (b - e,b +e) = Æ, что невозможно. Значит, предположение неверно и для последовательности существует только один предел.
. Поскольку yn®a, то найдется такой номер n1, что для n > n1 будет выполняться неравенство a - e < yn < a +e. С другой стороны, раз yn ® b, то найдется такой номер n2,что для n > n2 окажется b - e < yn < b +e. Если взять номер n большим и n1, и n2, то соответствующие значения yn последовательности {yn} будут одновременно принадлежать двум интервалам (a - e,a +e) и (b - e,b +e), которые не пересекаются, т.е. (a - e,a +e) ∩ (b - e,b +e) = Æ, что невозможно. Значит, предположение неверно и для последовательности существует только один предел. ,
,  ,
,  ,… попали в окрестность (a - e,a +e), т.е. a - e < yn < a +e " n > ne .
,… попали в окрестность (a - e,a +e), т.е. a - e < yn < a +e " n > ne . ,m¢ выберем наибольшее m = max(|y1|,|y2|,|y3|,....,
,m¢ выберем наибольшее m = max(|y1|,|y2|,|y3|,....,  ограничена, но предела не имеет. Действительно, по определению предела последовательности число a будет ее пределом, если в любой e-окрестности точки a содержится бесконечное множество членов этой последовательности, а вне ее – конечное. В данном случае в любой e-окрестности, например, единицы, e < 1, находится бесконечное множество членов последовательности, но и вне этой окрестности также находится бесконечное множество ее членов. Это означает, что последовательность не имеет предела.
ограничена, но предела не имеет. Действительно, по определению предела последовательности число a будет ее пределом, если в любой e-окрестности точки a содержится бесконечное множество членов этой последовательности, а вне ее – конечное. В данном случае в любой e-окрестности, например, единицы, e < 1, находится бесконечное множество членов последовательности, но и вне этой окрестности также находится бесконечное множество ее членов. Это означает, что последовательность не имеет предела. ограничена.
ограничена.  при всех n, и, тем не менее
при всех n, и, тем не менее 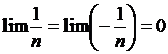 .Эта теорема дает возможность осуществлять предельный переход в неравенствах: из xn ³ yn можно заключить, что lim xn ³ lim yn.
.Эта теорема дает возможность осуществлять предельный переход в неравенствах: из xn ³ yn можно заключить, что lim xn ³ lim yn.