
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Местные гидравлические сопротивления
К этим сопротивлениям относятся резкие изменения формы граничных поверхностей потока (расширения, сужения, изгибы, изломы и т.п.). Общей зависимостью для определения потерь напора в местных сопротивлениях служит формула
или
где Общий характер этой зависимости для нескольких типов местных сопротивлений приведен на рис. 8.8. Эти кривые удовлетворительно описываются формулой вида
где
Рис. 8.8. Зависимость коэффициента местных сопротивлений от числа Рейнольдса: – тройник; Ñ – шаровой клапан;
к площади трубы
В табл. 8.3 приводятся постоянные Таблица 8.3 Значения
* Через 
В большинстве случаев местные сопротивления работают при больших числах Re или в условиях квадратичного режима, когда При проходе потока из трубы площадью
где
Формулы для определения коэффициента Таблица 8.4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 515. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
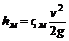 (8.16)
(8.16)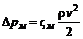 , (8.17)
, (8.17)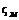 – коэффициент местного сопротивления, зависящий в общем случае от числа Re и конфигурации граничных поверхностей.
– коэффициент местного сопротивления, зависящий в общем случае от числа Re и конфигурации граничных поверхностей.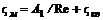 , (8.18)
, (8.18)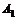 ,
, 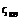 – постоянные, зависящие от геометрической формы местного сопротивления.
– постоянные, зависящие от геометрической формы местного сопротивления.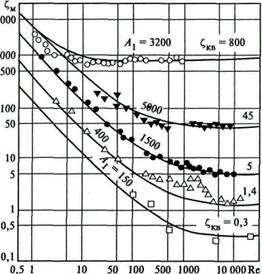
 – угольник 90°;
– угольник 90°; – разъемный клапан;
– разъемный клапан;  – диафрагма (при отношении площади отверстия
– диафрагма (при отношении площади отверстия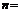 0,05)
0,05)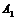 и
и 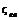 для некоторых местных сопротивлений
для некоторых местных сопротивлений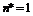
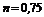
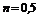
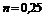
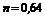
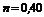
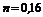
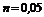
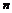 обозначено отношение площади проходного сечения, открытого задвижкой, или отверстия диафрагмы к площади сечения трубы.
обозначено отношение площади проходного сечения, открытого задвижкой, или отверстия диафрагмы к площади сечения трубы.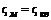 .
.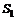 через диафрагму с площадью отверстия
через диафрагму с площадью отверстия 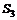 в трубу площадью
в трубу площадью 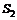 (табл. 8.4) формула для коэффициента сопротивления, отнесенного к скоростному напору за сопротивлением, имеет вид
(табл. 8.4) формула для коэффициента сопротивления, отнесенного к скоростному напору за сопротивлением, имеет вид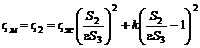 , (8.19)
, (8.19)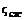 – коэффициент местного сопротивления при входе в диафрагму;
– коэффициент местного сопротивления при входе в диафрагму; 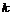 – поправочный коэффициент к потерям на расширение (при больших
– поправочный коэффициент к потерям на расширение (при больших 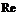 допустимо принимать
допустимо принимать 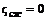 ,
, 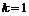 );
); 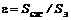 – коэффициент сжатия за диафрагмой, где
– коэффициент сжатия за диафрагмой, где 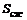 – площадь сечения струи за диафрагмой после выхода в трубу с сечением
– площадь сечения струи за диафрагмой после выхода в трубу с сечением 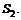 Он имеет значения:
Он имеет значения: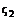 приведены в табл. 8.4.
приведены в табл. 8.4.