
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчетные формулы для гидравлического коэффициента трения
Сжимаемость газов мало влияет на зависимость
Рис. 8.4. Зависимость гидравлического коэффициента трения для гладкой трубы от числа Рейнольдса: расчет по формуле Прандтля-Никурадзе
Рис. 8.5. Влияние числа Маха на гидравлический коэффициент трения при дозвуковом течении газа в гладкой трубе:
Внутренняя структура течения в круглых трубах зависит от режимов течения. При стабилизированном ламинарном течении распределение местных скоростей подчиняется параболическому закону
или в безразмерном виде
где р – давление; Средняя скорость в 2 раза меньше максимальной: 
Из уравнения Бернулли, составленного для граничных сечений участка
откуда вытекает, что
где Стабилизированное течение устанавливается лишь на некотором расстоянии от входа в трубу, за пределами начального участка, длина которого для круглой трубы Падение давления на начальном участке не подчиняется формуле Пуазейля, но приближенно может быть определено по формуле
где Разрушение ламинарного режима в трубе и переход к турбулентному режиму происходит при достижении критического числа Рейнольдса. Для круглых труб это значение составляет приблизительно 2300. При При стабилизированном турбулентном течении в трубах распределение местных осредненных скоростей описывается полуэмпирическими или эмпирическими формулами. Наиболее известные из них: ● логарифмическая формула для гладкостенного режима течения
где Другая форма этой зависимости имеет вид
где Средняя скорость связана с максимальной соотношением
● универсальная логарифмическая формула для всех турбулентных режимов в шероховатых трубах
где функция ● степенная формула (эмпирическая)
где показатель
Рис. 8.6. Вид функции определяющей закон распределения скоростей в шероховатых трубах
Рис. 8.7. Зависимость гидравлического коэффициента трения от числа Рейнольдса для труб некруглого сечения: 1 – ламинарное течение, |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 617. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
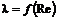 , о чем свидетельствуют опытные данные, приведенные на рис. 8.4. Однако в области чисел Маха М, близких к 1, наблюдаются заметные отклонения значений
, о чем свидетельствуют опытные данные, приведенные на рис. 8.4. Однако в области чисел Маха М, близких к 1, наблюдаются заметные отклонения значений  для газа от значений этого коэффициента для несжимаемой жидкости (рис. 8.5).
для газа от значений этого коэффициента для несжимаемой жидкости (рис. 8.5).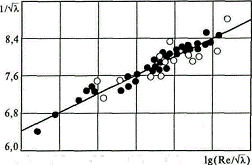
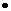 – дозвуковое течение;
– дозвуковое течение; 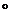 – сверхзвуковое течение;
– сверхзвуковое течение;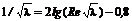
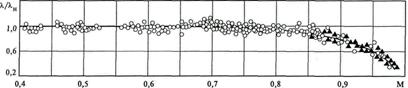
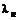 – коэффициенты трения для газа и несжимаемой жидкости;
– коэффициенты трения для газа и несжимаемой жидкости; 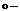 опыты МЭИ;
опыты МЭИ;  – опыты МО ЦКТИ
– опыты МО ЦКТИ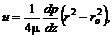 (8.5)
(8.5)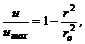 (8.6)
(8.6)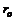 – радиус трубы;
– радиус трубы;  – координата, отсчитываемая вдоль оси трубы вниз по течению;
– координата, отсчитываемая вдоль оси трубы вниз по течению; 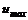 – максимальная скорость.
– максимальная скорость.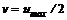 . Падение давления
. Падение давления  на участке горизонтальной трубы длиной
на участке горизонтальной трубы длиной 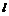 определяют по формуле Пуазейля
определяют по формуле Пуазейля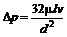 . (8.7)
. (8.7)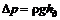 , где
, где 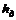 – потери напора и, следовательно,
– потери напора и, следовательно,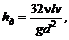 (8.8)
(8.8)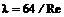 , где
, где 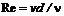 . Для наклонной трубы падение гидродинамического напора:
. Для наклонной трубы падение гидродинамического напора: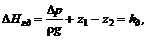 (8.9)
(8.9)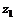 ,
, 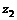 – отметки центров тяжести сечений трубы в начале и конце участка
– отметки центров тяжести сечений трубы в начале и конце участка 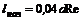 .
.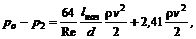 (8.10)
(8.10)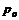 – давление в резервуаре, к которому присоединена труба;
– давление в резервуаре, к которому присоединена труба; 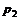 – давление в конце начального участка.
– давление в конце начального участка.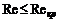 наблюдается устойчивый ламинарный режим; при
наблюдается устойчивый ламинарный режим; при 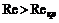 возможно появление турбулентности, но не исключено и сохранение ламинарного режима, который является неустойчивым. Для труб некруглого сечения критическое число Рейнольдса приблизительно равно 2000, причем
возможно появление турбулентности, но не исключено и сохранение ламинарного режима, который является неустойчивым. Для труб некруглого сечения критическое число Рейнольдса приблизительно равно 2000, причем 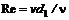 , где
, где 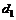 – гидравлический диаметр, определяемый соотношением
– гидравлический диаметр, определяемый соотношением 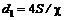 , в котором – смоченный периметр сечения
, в котором – смоченный периметр сечения  трубы.
трубы.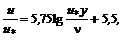 (8.11)
(8.11)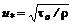 – динамическая скорость;
– динамическая скорость;  – касательное напряжение на стенке;
– касательное напряжение на стенке; 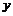 – расстояние от стенки.
– расстояние от стенки.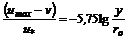 , (8.12)
, (8.12)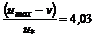 ; (8.13)
; (8.13)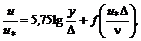 (8.14)
(8.14)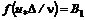 определяется графиком, приведенном на рис. 8.6;
определяется графиком, приведенном на рис. 8.6;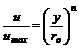 , (8.15)
, (8.15)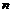 в зависимости от числа Re изменяется от 1/6 до 1/10. Значение, соответствующее гладкостенному режиму (при
в зависимости от числа Re изменяется от 1/6 до 1/10. Значение, соответствующее гладкостенному режиму (при 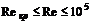 ):
): 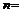 1/7.
1/7.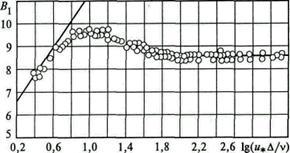
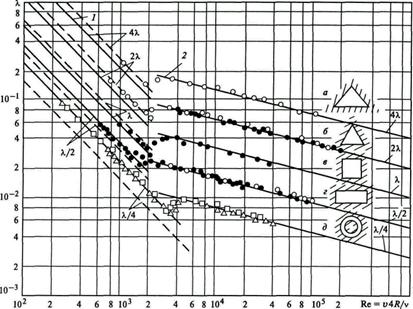
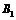 ,
,
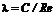 ; 2 – турбулентное течение
; 2 – турбулентное течение 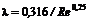 ; _ _ – ламинарное течение в круглой трубе,
; _ _ – ламинарное течение в круглой трубе, 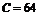 ; а – равнобедренный прямоугольный треугольник,
; а – равнобедренный прямоугольный треугольник, 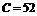 ; б – равносторонний треугольник,
; б – равносторонний треугольник, 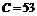 ; в – квадрат,
; в – квадрат, 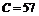 ; г – прямоугольник (
; г – прямоугольник ( 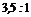 ),
), 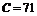 ; д – кольцевая щель,
; д – кольцевая щель, 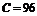 ;
; 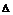 –
– 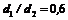 ; –
; –  , измерения Коха и Файнда
, измерения Коха и Файнда