
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Коэффициенты истечения через насадки
Примечание. Для всех насадков коэффициенты даны применительно к выходному сечению.
Вопросы для самопроверки: 1. Какой физический закон выражает уравнение Бернулли? Запишите уравнение Бернулли для двух сечений потока вязкой жидкости и дайте его геометрическую и энергетическую интерпретацию. 2. От каких факторов зависит коэффициент гидравлического сопротивления? 3. Какие зоны сопротивлений турбулентного режима Вы знаете? 4. Чем обусловлено наличие местных потерь напора? 5. Что называется гидравлическим ударом в трубопроводе? Запишите формулы Жуковского для гидравлического удара. 6. Какие виды насадков Вы знаете? Опишите их технические характеристики и область применения.
ЛЕКЦИЯ 9. МОДЕЛИРОВАНИЕ ЯВЛЕНИЙ В ГИДРОГАЗОДИНАМИКЕ Основные понятия теории моделирования Моделированием называется метод экспериментального изучения модели явления вместо натурного явления. Модель выбирают так, чтобы результаты эксперимента можно было распространить на натурное явление. Пусть моделируется поле величины w. Тогда при точном моделировании в сходственных точках модели и натурного объекта должно соблюдаться условие
где В случае приближенного моделирования получим 
Отношение Если степень искажения
Метод аналогий
Если два физических явления различной физической природы описываются тождественными уравнениями и условиями однозначности (краевыми или в стационарном случае граничными условиями), представленными в безразмерной форме, то явления называются аналогичными. При этих же условиях явления одной физической природы называются подобными. Несмотря на то, что аналогичные явления имеют различную физическую природу, они относятся к одному индивидуальному обобщенному случаю. Это обстоятельство позволило создать весьма удобный метод аналогий для изучения физических явлений. Сущность его состоит в следующем: обследованию подвергается не изучаемое явление, для которого трудно или невозможно измерить искомые величины, а специально подобранное, аналогичное изучаемому. В качестве примера рассмотрим электротепловую аналогию. В этом случае изучаемое явление – стационарное температурное поле, а его аналогия – стационарное поле электрического потенциала. Уравнение теплопроводности
где
где Если созданы граничные условия для потенциала, аналогичные условиям для температуры, то в безразмерной форме они будут также тождественны. Электротепловая аналогия широко используется при изучении процессов теплопроводности. Например, температурные поля лопаток газовых турбин были измерены этим методом. Анализ размерностей Иногда приходится изучать процессы, которые еще не описаны дифференциальными уравнениями. Единственный путь изучения – эксперимент. Результаты эксперимента целесообразно представлять в обобщенной форме, но для этого нужно уметь находить безразмерные комплексы, характерные для такого процесса Анализ размерностей – это метод составления безразмерных комплексов в условиях, когда изучаемый процесс еще не описан дифференциальными уравнениями. Все физические величины можно разделить на первичные и вторичные. Для процессов теплообмена за первичные обычно выбирают следующие: длину L, массу m, время t, количество теплоты Q, избыточную температуру Формулы размерности вторичных величин имеют вид степенных одночленов. Например, формула размерности для коэффициента теплоотдачи
где Q – количество теплоты. Пусть известны все физические величины, существенные для изучаемого процесса. Требуется найти безразмерные комплексы. Составим произведение из формул размерностей всех существенных для процесса физических величин в некоторых неопределенных пока степенях; очевидно, оно будет степенным одночленом (для процесса). Предположим, что его размерность (степенного одночлена) равна нулю, т. е. показатели степеней первичных величин, входящих в формулу размерностей, сократились, тогда степенной одночлен (для процесса) можно представить в форме произведения безразмерных комплексов из размерных величин. Значит, если составить произведение из формул размерностей, существенных для процессов физических величин в неопределенных степенях, то из условия равенства нулю суммы показателей степеней первичных величин этого степенного одночлена можно определить искомые безразмерные комплексы. Покажем эту операцию на примере периодического процесса теплопроводности в твердом теле, омываемом жидким теплоносителем. Будем считать, что дифференциальные уравнения для рассматриваемого процесса неизвестны. Требуется найти безразмерные комплексы. Существенными физическими величинами для изучаемого процесса будут следующие: характерный размер l (м), теплопроводность твердого тела
Показатель степени при первичной величине называется размерностью вторичной величины по отношению к данной первичной. Заменим физические величины (кроме Q) их формулами размерности, в результате получим
В данном случае показатели степени Приравняем нулю показатели степеней одночлена: для длины a – b – 3i – 2k = 0; (9.8) для количества теплоты Q
для времени
для температуры
для массы m
Всего существенных величин семь, уравнений для определения показателей пять, значит, только два показателя, например b и k, могут быть выбраны произвольно. Выразим все показатели степеней через b и k. В результате получим из выражений: (9.8), (9.9), (9.12)
(9.9) f = – b – k; (9.14) (9.10) r=b + k; (9.15) (9.11) и (9.9) n = b + f + k = b + (– b – k) + k = 0; (9.16) (9.12) и (9.9) i = f = – b – k. (9.17) Теперь одночлен можно представить в форме
Так как показатели b и k могут быть выбраны произвольно, положим: 1)
откуда
обозначим 2) b = 0, k = 1, при этом запишем
обозначим
Найдем отношение
Итак, методом анализа размерностей найдены безразмерные комплексы. В рассматриваемом случае ими оказались числа подобия Фурье Введем безразмерные – искомую переменную
Правильность полученного результата подтверждает так называемая
Вопросы для самопроверки: 1. В чем сущность метода аналогий? 2. В чем сущность метода анализа размерностей? Сформулируйте π-теорему. 3. Какие критерии гидродинамического подобия Вам известны? ЛЕКЦИЯ 10. РЕЖИМЫ ТЕЧЕНИЯ ВЯЗКОЙ СРЕДЫ. ПОГРАНИЧНЫЙ СЛОЙ |
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 561. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





 , (9.1)
, (9.1) – масштаб моделирования.
– масштаб моделирования. (9.2)
(9.2) называется степенью искажения.
называется степенью искажения. не превосходит точности измерения, то приближенное моделирование не отличается от точного. Нельзя заранее сделать так, чтобы величина
не превосходит точности измерения, то приближенное моделирование не отличается от точного. Нельзя заранее сделать так, чтобы величина 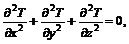 (9.3)
(9.3) – абсолютная температура, и уравнение электрического потенциала
– абсолютная температура, и уравнение электрического потенциала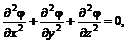 (9.4)
(9.4)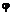 – электрический потенциал, аналогичны. В безразмерной форме эти уравнения будут тождественны.
– электрический потенциал, аналогичны. В безразмерной форме эти уравнения будут тождественны.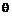 . Тогда вторичными будут такие величины, как коэффициент теплоотдачи
. Тогда вторичными будут такие величины, как коэффициент теплоотдачи 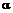 , температуропроводность a и т. п.
, температуропроводность a и т. п. (9.5)
(9.5) , (Дж/(м К)), удельная теплоемкость твердого тела с (Дж/(кг К)), плотность твердого тела
, (Дж/(м К)), удельная теплоемкость твердого тела с (Дж/(кг К)), плотность твердого тела 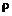 (кг/м3), коэффициент теплообмена (теплоотдачи)
(кг/м3), коэффициент теплообмена (теплоотдачи)  , (с), характерная избыточная температура
, (с), характерная избыточная температура  (9.6)
(9.6) (9.7)
(9.7) имеют значения, при которых Q выпадает из уравнения.
имеют значения, при которых Q выпадает из уравнения. 0; (9.9)
0; (9.9) = 0; (9.10)
= 0; (9.10)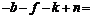 0; (9.11)
0; (9.11) 0. (9.12)
0. (9.12) ; (9.13)
; (9.13) (9.18)
(9.18) ,
,  , при этом запишем
, при этом запишем , (9.19)
, (9.19) , (9.20)
, (9.20) ;
; (9.21)
(9.21) . (9.22)
. (9.22) (9.23)
(9.23) и Био
и Био  .
. и независимую переменную
и независимую переменную  (одномерный случай). Тогда искомую обобщенную зависимость можно представить в форме
(одномерный случай). Тогда искомую обобщенную зависимость можно представить в форме . (9.24)
. (9.24)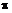 -теорема Бэкингема, которая формулируется так: число безразмерных комплексов равно числу физических величин, существенных для процесса, минус число первичных величин.
-теорема Бэкингема, которая формулируется так: число безразмерных комплексов равно числу физических величин, существенных для процесса, минус число первичных величин.