
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
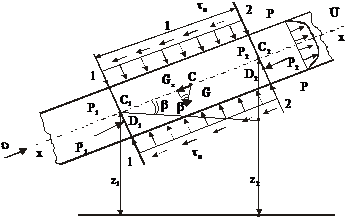
Одномерное движение жидкости в трубеРассмотрим одномерное движение жидкости в трубе на участке 1-1 (рис. 7.1).
Рис. 7.1. Движение жидкости на участке трубы
При равномерном движении эпюры скоростей Составим уравнение равновесия суммы проекций внешних сил на ось движения Х, действующих на отсек 1-2, в виде Силы давления приложены в центрах давления По смоченной боковой поверхности потока По всей смоченной поверхности действуют силы трения Силы тяжести жидкости
Из треугольника
и
Проекции всех сил дают уравнение
что после перегруппировки и деления на
Поскольку скоростной напор в равномерном движении постоянен, то есть
где Величина
Величина касательных напряжений в большинстве задач квадратично зависит от скорости
где Из предыдущего уравнения следует 
или
Учитывая, что
где Обозначив
которая называется формулой Вейсбаха. Это обобщение формулы Дарси-Вейсбаха дает возможность рассчитывать местные сопротивления. Из формулы Дарси-Вейсбаха (7.11) с учетом
где
Режимы движения жидкости. Число Рейнольдса
Механизм перемещения отдельных частиц изучался О. Рейнольдсом путем их визуализации. Струйка жидкости подкрашивалась и ее характер фиксировался при разных средних скоростях В результате установлено, что до некоторой скорости
Рис. 7.2. Опыты Рейнольдса
В области до критической скорости режим движения ламинарный (слоистый). Затем появляются поперечные пульсации и движение становится вихревым. Наконец, с ростом скорости процесс становится хаотическим и режим становится турбулентным. Обобщение условий смены режима движения определяется безразмерным параметром, называемым числом Рейнольдса:
где Критические точки перехода от одного режима движения к другому характеризуются нижним и верхним числами Рейнольдса:
причем
Формула Пуазейля
При ламинарном режиме движения касательное напряжение в круглой трубе при равномерном движении имеет вид
где Распределение давлений в трубе подчиняется гидростатическому закону. Касательные напряжения по закону Ньютона равны
поэтому с учетом предыдущего и интегрирования
Из условия нулевой скорости на стенках трубы
поэтому
Эпюра скоростей в живом сечении будет параболоидом вращения, и максимум достигается на оси трубы
Элементарный расход в кольцевом сечении равен
Интегрирование в пределах от
Средняя скорость потока
Потери напора определяются из условия
Это формула Пуазейля.
Длина пути перемешивания
Из формулы Дарси-Вейсбаха (7.11) и формулы Пуазейля (7.26) получим
При турбулентном режиме закон Ньютона может быть модернизирован по Буссинеску
Прандтль ввел понятие длины пути перемещения и дал формулу
где l – осредненное значение пути перемешивания, аналогичное длине свободного пробега молекулы в кинетической теории газов. В теории турбулентности вводится понятие динамической скорости
где По Прандтлю длина пути перемешивания равна
где
Вопросы для самопроверки: 1. Какие существуют режимы движения жидкости? Охарактеризуйте их. 2. Как определить режим движения жидкости не визуально, а расчетным путем? 3. Как записывается основное уравнение равномерного движения жидкости? 4. Какие два вида потерь напора Вы знаете? Запишите формулы Дарси-Вейсбаха для их вычисления.
ЛЕКЦИЯ 8.ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 562. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
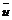 одинаковы в поперечных сечениях по длине трубы.
одинаковы в поперечных сечениях по длине трубы.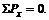

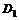 и
и 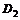 и равны
и равны 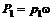 и
и 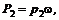 где
где 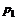 и
и 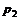 – давления в центрах тяжести сечений
– давления в центрах тяжести сечений 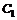 и
и 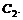
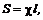 где
где  – смоченный периметр, а l – длина отсека, действуют давления
– смоченный периметр, а l – длина отсека, действуют давления  , направленные по нормали, и касательные напряжения
, направленные по нормали, и касательные напряжения 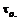
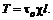
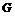 в отсеке 1-2 в проекции на ось Х-Х равны
в отсеке 1-2 в проекции на ось Х-Х равны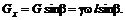 (7.1)
(7.1)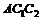 и силового треугольника с гипотенузой
и силового треугольника с гипотенузой 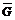 найдем
найдем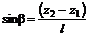 (7.2)
(7.2)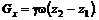 (7.3)
(7.3)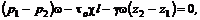 (7.4)
(7.4)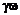 позволяет записать
позволяет записать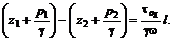 (7.5)
(7.5)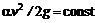 , то потери напора равны
, то потери напора равны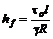 , (7.6)
, (7.6)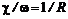 , а
, а  – гидравлический радиус.
– гидравлический радиус.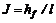 – гидравлический уклон, поэтому основное уравнение равномерного движения будет иметь вид
– гидравлический уклон, поэтому основное уравнение равномерного движения будет иметь вид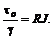 (7.7)
(7.7)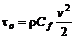 , (7.8)
, (7.8)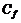 – коэффициент местного трения.
– коэффициент местного трения.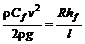 (7.9)
(7.9)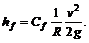 (7.10)
(7.10)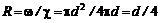 , и обозначив
, и обозначив 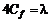 , получим формулу Дарси-Вейсбаха для потерь по длине
, получим формулу Дарси-Вейсбаха для потерь по длине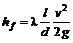 , (7.11)
, (7.11) – коэффициент трения, или коэффициент Дарси.
– коэффициент трения, или коэффициент Дарси.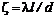 , получим формулу
, получим формулу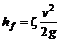 , (7.12)
, (7.12)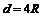 получим формулу Шези
получим формулу Шези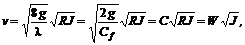 (7.13)
(7.13)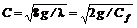 – коэффициент Шези с размерностью в СИ
– коэффициент Шези с размерностью в СИ 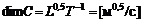 ;
; 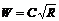 – модуль скорости с размерностью
– модуль скорости с размерностью 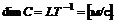
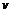 (рис. 7.2).
(рис. 7.2).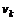 график функции
график функции 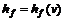 является прямой и потери энергии линейно возрастают с возрастанием скорости. Затем функция
является прямой и потери энергии линейно возрастают с возрастанием скорости. Затем функция 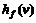 становится квадратичной
становится квадратичной 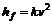 . Области разделяются критической скоростью
. Области разделяются критической скоростью 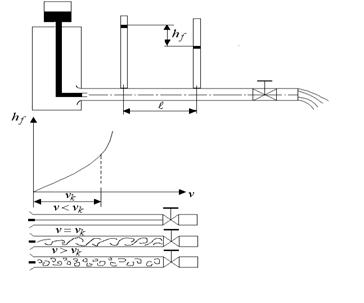
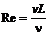 , (7.14)
, (7.14) – кинематическая вязкость.
– кинематическая вязкость.
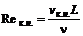 и
и 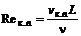 , (7.15)
, (7.15)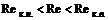 (7.16)
(7.16)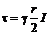 , (7.17)
, (7.17)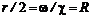 – гидравлический радиус.
– гидравлический радиус.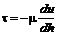 , (7.18)
, (7.18)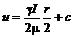 . (7.19)
. (7.19)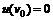 получим
получим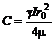 , (7.20)
, (7.20)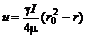 . (7.21)
. (7.21)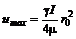 . (7.22)
. (7.22)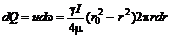 . (7.23)
. (7.23)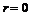 до
до 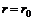 дает
дает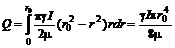 . (7.24)
. (7.24)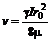 . (7.25)
. (7.25)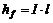 , поэтому
, поэтому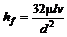 . (7.26)
. (7.26)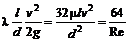 . (7.27)
. (7.27)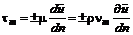 . (7.28)
. (7.28)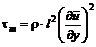 , (7.29)
, (7.29)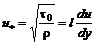 , (7.30)
, (7.30)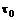 – касательное напряжение на стенке.
– касательное напряжение на стенке.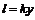 , (7.31)
, (7.31)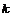 – постоянная, поэтому распределение скоростей в турбулентном потоке равно
– постоянная, поэтому распределение скоростей в турбулентном потоке равно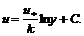 (7.32)
(7.32)