Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обтекание круглого цилиндра
Комплексный потенциал, включающий сумму потенциалов плоскопараллельного оси Х потока и диполя, можно записать
Отделив мнимую и вещественную части, запишем
Выражения для потенциала скорости и функции тока с учетом
Следовательно, уравнение линии тока будет иметь вид
Нулевая линия тока
Второе уравнение представляет собой окружность радиуса
с центром в начале координат. Первое соответствует оси абсцисс (рис. 6.7).
Рис. 6.7. Линии тока при обтекании круглого цилиндра
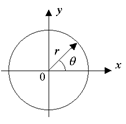
Рис. 6.8. Цилиндрические координаты (полярные в сечении) Заменив нулевую линию тока твердой стенкой без изменения характера движения потока, получим обтекание круглого цилиндра. В цилиндрических координатах запишем равенства
поэтому
Проекции скорости будут
На поверхности цилиндра
Точки, в которых скорость равна нулю при обтекании цилиндра, соответствуют Из уравнения Бернулли для нулевой линии тока получим
или
где Вводя коэффициент давления
 и подставляя
Поэтому
Рис. 6.9. Распределение коэффициента давления
Обтекание реальной жидкостью круглого цилиндра ведет к несимметричному распределению давления. Вид кривой распределения давления зависит от числа Рейнольдса Re. Проекции сил давления, действующего на элементарную площадку
Поскольку
и
то
Учитывая
получим Аналогично доказывается, что и Отсутствие силы сопротивления для тел, независимо от их формы, обтекаемых потоком идеальной жидкости, в гидродинамике называется парадоксом Даламбера.
Вопросы для самопроверки: 1. Что называется функцией тока? 2. Какова общая форма записи уравнения линий тока? 3. Какова форма записи уравнений линий тока и эквипотенциалей для плоскопараллельного потока? 4. Какими уравнениями определяются линии тока и эквипотенциали источника и стока? 5. Какими выражениями определяются проекции скорости потока при обтекании цилиндра?
ЛЕКЦИЯ 7.ГИДРОМЕХАНИКА ТРУБОПРОВОДОВ |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 568. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
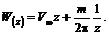 (6.54)
(6.54)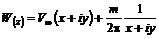 . (6.55)
. (6.55)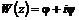 :
: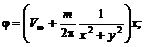 (6.56)
(6.56)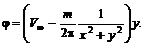 (6.57)
(6.57)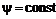 или
или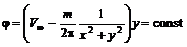 (6.58)
(6.58)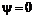 задается двумя уравнениями:
задается двумя уравнениями: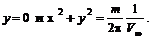 (6.59)
(6.59)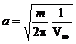 (6.60)
(6.60)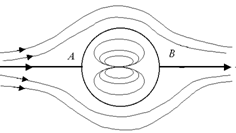
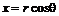 ,
, 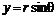 ,
, 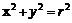 (рис. 6.8) и
(рис. 6.8) и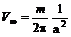 , (6.61)
, (6.61)
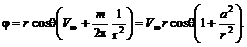 (6.62)
(6.62)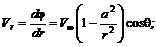 (6.63)
(6.63)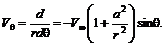 (6.64)
(6.64)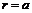 и
и 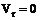 , а
, а 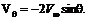 (6.65)
(6.65)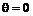 и
и 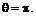 Максимальные значения скоростей соответствуют
Максимальные значения скоростей соответствуют 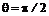 и
и 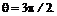
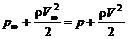 (6.67)
(6.67)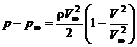 , (6.68)
, (6.68) – давление в любой точке на поверхности цилиндра.
– давление в любой точке на поверхности цилиндра.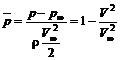 (6.69)
(6.69)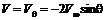 , получим
, получим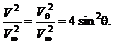 (6.70)
(6.70)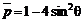 (6.71)
(6.71)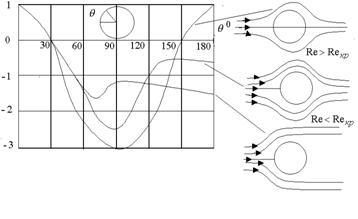
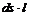 (единичной длины), будут равны:
(единичной длины), будут равны: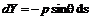 ;
; 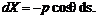 (6.72)
(6.72)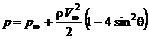 (6.73)
(6.73)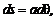 (6.74)
(6.74)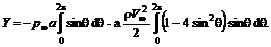 (6.75)
(6.75)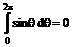 и
и 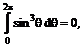 (6.76)
(6.76)