Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Для решения задач гидродинамики
В теории комплексной переменной связь между функциями При этом комплексная величина
Рис. 6.2. Определение комплексной переменной
Таким образом, существует функция комплексной переменной
Функция Производная
или
С учетом условий
Величина и направление скорости
Производная от комплексного потенциала по координате равна скорости по абсолютной величине, а по направлению совпадает с зеркальным отображением вектора скорости относительно вещественной оси. Величина Плоскость Значение контурного интеграла равно
но
а
Здесь Для действительной части получим
а для мнимой
Можно поставить две задачи: 1) по заданному комплексному потенциалу найти  2) зная контур обтекаемого тела и значение скорости на бесконечности, найти комплексный потенциал. В качестве примеров рассмотрим простейшие потенциальные потоки.
Плоскопараллельный поток
Пусть комплексный потенциал имеет вид
Если
Рис. 6.3. Поток при действительном
Из
а линии тока
Проекции скоростей равны
При минимальных числах
Эквипотенциальные линии и линии тока
Проекции скоростей будут соответствовать
Если
(6.30) Потенциал скорости
а проекции скоростей равны
Уравнениями линий тока и эквипотенциалей будут
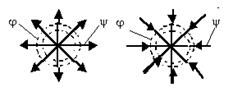
Источник и сток Вторым примером комплексного потенциала является функция
При вещественном
Потенциал скорости и функция тока
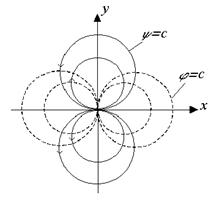
Линии тока и эквипотенциали источника и стока (рис. 6.4) определяются уравнениями
Рис. 6.4. Линии тока и эквипотенциали источника и стока
В цилиндрической системе координат
Если Объемный расход источника (стока)
определяет мощность (обильность) источника (стока). Комплексный потенциал в этом случае равен
Вихрь
Если
поэтому
где Тогда
Составляющие скорости
Циркуляция вдоль замкнутой линии
т.е.
Комплексный потенциал потока с циркуляцией равен
Рис. 6.5. Линии тока и эквипотенциали вихря
Величина скорости
Движение соответствует циркуляционному потоку вокруг вихревой нити.
Диполь Комплексный потенциал
после подстановки
откуда
Линии тока и эквипотенциали
Это семейства окружностей с центрами, расположенными на оси
Рис. 6.6. Диполь
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 573. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
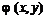 и
и 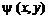 называется условиями Коши-Римана.
называется условиями Коши-Римана.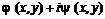 является комплексной переменной
является комплексной переменной  , равной
, равной 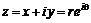 (рис. 6.2).
(рис. 6.2).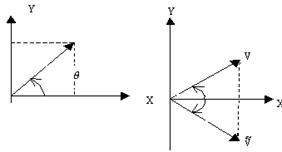
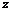 и
и 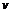
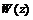 , вещественная и мнимая части которой будут
, вещественная и мнимая части которой будут  и
и  , т.е.
, т.е.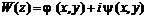 . (6.10)
. (6.10)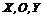 , заданной координатой z, т.е.
, заданной координатой z, т.е.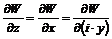 (6.11)
(6.11)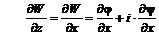 ; (6.12)
; (6.12)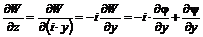 . (6.13)
. (6.13)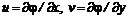 и
и 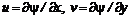 получим
получим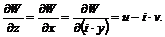 (6.14)
(6.14)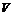 в комплексной плоскости (рис. 6.2) определится формулой
в комплексной плоскости (рис. 6.2) определится формулой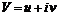 . (6.15)
. (6.15)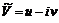 называется сопряженной скоростью.
называется сопряженной скоростью.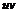 является плоскостью годографа скорости.
является плоскостью годографа скорости.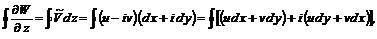 (6.16)
(6.16)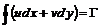 , (6.17)
, (6.17)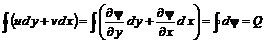 . (6.18)
. (6.18)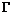 – циркуляция скорости по замкнутому контуру;
– циркуляция скорости по замкнутому контуру; 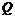 – объемный расход через замкнутый контур.
– объемный расход через замкнутый контур.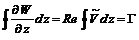 , (6.19)
, (6.19)
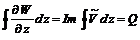 . (6.20)
. (6.20)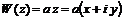 . (6.21)
. (6.21)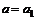 вещественно (рис. 6.3), то
вещественно (рис. 6.3), то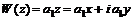 . (6.22)
. (6.22)
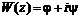 находим
находим 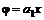 ,
, 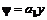 и эквипотенциали
и эквипотенциали 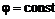 , имеющие вид
, имеющие вид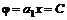 , (6.23)
, (6.23)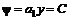 . (6.24)
. (6.24)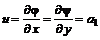 ; (6.25)
; (6.25)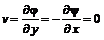 . (6.26)
. (6.26)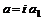 (
( 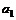 – вещественно)
– вещественно)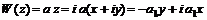 . (6.27)
. (6.27)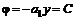 и
и 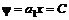 . (6.28)
. (6.28)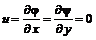 и
и 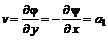 . (6.29)
. (6.29)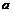 – комплексное число, равное
– комплексное число, равное 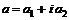 (
( 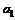 и
и 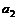 – вещественные положительные числа), то
– вещественные положительные числа), то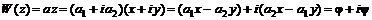 .
.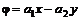 и
и 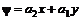 , (6.31)
, (6.31)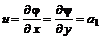 и
и 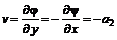 . (6.32)
. (6.32)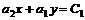 или
или 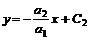 ; (6.33)
; (6.33)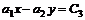 или
или 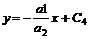 . (6.34)
. (6.34) . (6.35)
. (6.35)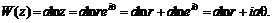 (6.36)
(6.36)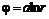 и
и 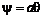 . (6.37)
. (6.37)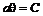 и
и 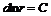 .
.
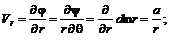 (6.38)
(6.38)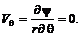 (6.39)
(6.39)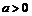 , то возникает источник, а при
, то возникает источник, а при 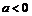 – сток. Начало координат является точкой, в которой скорость равна бесконечности.
– сток. Начало координат является точкой, в которой скорость равна бесконечности.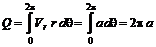 (6.40)
(6.40)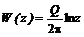 . (6.41)
. (6.41)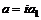 и
и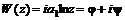 , (6.42)
, (6.42)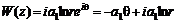 , (6.43)
, (6.43)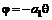 и
и 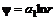 , а уравнения линий тока и эквипотенциалей
, а уравнения линий тока и эквипотенциалей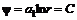 и
и 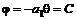 (рис. 6.5). (6.44)
(рис. 6.5). (6.44)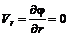 и
и 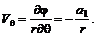 (6.45)
(6.45)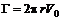 или
или 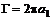 , (6.46)
, (6.46)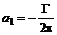 . (6.47)
. (6.47)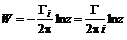 . (6.48)
. (6.48)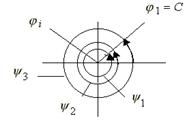
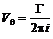 . (6.49)
. (6.49)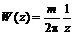 (6.50)
(6.50)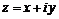 даст
даст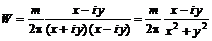 , (6.51)
, (6.51)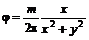 и
и 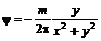 . (6.52)
. (6.52)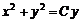 ;
; 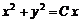 . (6.53)
. (6.53)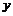 и
и 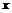 .
.