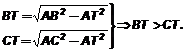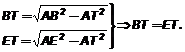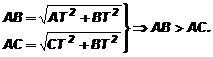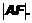Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
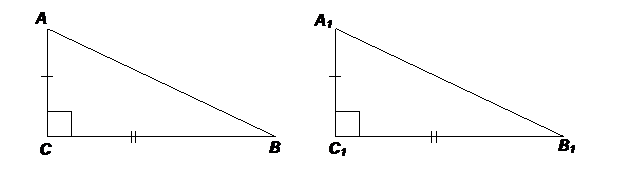
Возьмем на прямой р точку В, отличную от точки С, и соединим точки А и В отрезком.Стр 1 из 25Следующая ⇒ Билет № 1. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная. 1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
4. Если катет и противолежащий острый угол одного треугольника соответственно равны катету и противолежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников). Доказывается аналогично предыдущей теореме ─ следствие из II признака равенства треугольников. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
Доказательство: 1. Т. к. ÐС = ÐС1, то DАВС можно наложить на DА1В1С1 так, что вершина С совместится с вершиной С1, а стороны СА и СВ наложатся соответственно на лучи СА1 и СВ1. 2. Т. к. СА = С1А1, то вершина А совместится с вершиной А1. Остается доказать, что совместятся точки В и В1. 3. Предположим, что точки В и В1 не совместятся. Рассмотрим Δ А1В1В2 – равнобедренный, так как АВ = A1B1 Þ А1В2 = A1B1. Тогда ÐA1B1В2 = ÐA1В2B1. Заметим, что ÐA1B1С1 - острый угол прямоугольного треугольника А1В1С1, а ÐA1B1В2, смежный с ним, - тупой. Поскольку в треугольнике не может быть двух тупых углов, то это невозможно. Значит, точки В и В1 совместятся.  Пусть р – любая прямая и точка А не лежит на ней. Из точки А опустим перпендикуляр АС на прямую р.
Возьмем на прямой р точку В, отличную от точки С, и соединим точки А и В отрезком. Определение 2. Отрезок АВ называется наклонной, проведенной из точки А на прямую р, а отрезок СВ называется проекцией наклонной АВ на прямую р. Наклонная, проекция наклонной и перпендикуляр являются гипотенузой и катетами прямоугольного треугольника АВС. По т-ме Пифагора
Теорема 1 (прямая). Если из одной точки проведены две наклонные к прямой, то большая наклонная имеет большую проекцию, меньшая наклонная – меньшую проекцию, равные наклонные имеют равные проекции. Доказательство: 1) Рассмотрим DАВТ и DАСТ. ÐАТВ = ÐАТС = 90°; АТ – общая; AB > AC. Тогда по теореме Пифагора 2) Рассмотрим DАВТ и DАЕТ. ÐАТВ = ÐАТЕ = 90°; АТ – общая; AB = AЕ. Тогда по теореме Пифагора Теорема 2 (обратная). Если из одной точки проведены две наклонные к прямой, то больше та наклонная, проекция которой больше. Доказательство: Рассмотрим DАВТ и DАСТ. ÐАТВ = ÐАТС = 90°; АТ – общая; BТ > CТ. Тогда по теореме Пифагора Определение 3. Расстоянием от точки А до фигуры F называется кратчайший отрезок, соединяющий любую граничную точку фигуры F с точкой А. Расстояние от точки А до фигуры F обозначается |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 230. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 2. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).
2. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).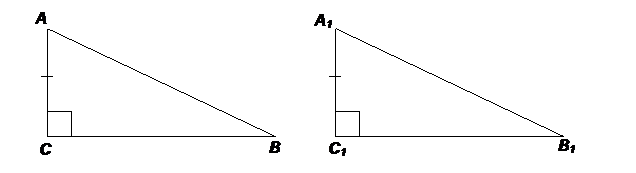
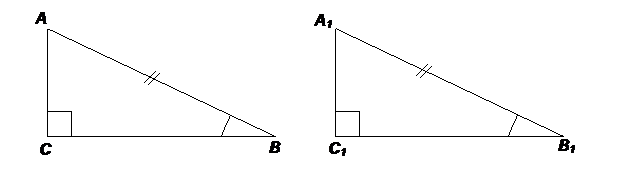
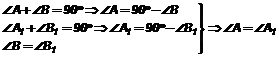 ─ следствие из 2 признака равенства треугольников.
─ следствие из 2 признака равенства треугольников.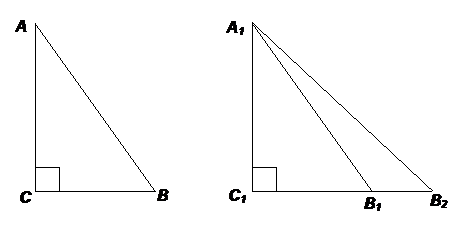
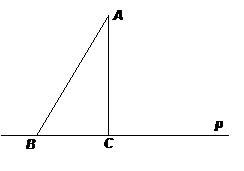 Определение 1. Точка С называется проекцией точки А на прямую р. Если точка А лежит на прямой, то ее проекцией на эту прямую является сама точка А. Точка С также называется основанием перпендикуляра АС.
Определение 1. Точка С называется проекцией точки А на прямую р. Если точка А лежит на прямой, то ее проекцией на эту прямую является сама точка А. Точка С также называется основанием перпендикуляра АС.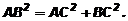 Поэтому
Поэтому 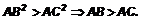 Аналогично
Аналогично 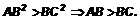
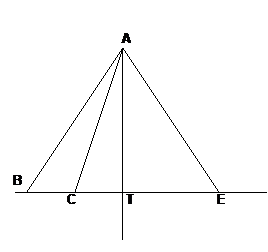 Свойство наклонной. Если из одной и той же точки проведены к некоторой прямой перпендикуляр и наклонная, то перпендикуляр и проекция наклонной всегда короче наклонной.
Свойство наклонной. Если из одной и той же точки проведены к некоторой прямой перпендикуляр и наклонная, то перпендикуляр и проекция наклонной всегда короче наклонной.