
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Число k, равное отношению сходственных сторон, называется коэффициентом подобия.Теорема об отношении площадей подобных многоугольников. Площади подобных многоугольников относятся как квадраты сходственных сторон. Доказательство: Подобные многоугольники можно разложить на одинаковое число подобных и одинаково расположенных треугольников. Для доказательства этой теоремы возьмем внутри многоугольника ABCDE произвольную точку О и соединим ее со всеми вершинами. Тогда многоугольник ABCDE разобьется на столько треугольников, сколько в нем сторон. Выберем один из них, например, DAOB, и на сходственной стороне A1B1 другого многоугольника построим углы О1А1В1 и О1В1А1, соответственно равные углам ОАВ и ОВА. Точку пересечения О1 соединим с прочими вершинами многоугольника А1В1С1D1E1. Тогда и этот многоугольник разобьется на столько же треугольников. Докажем, что треугольники первого многоугольника соответственно подобны треугольникам второго многоугольника. Из определения подобных многоугольников: Из подобия треугольников АОВ и А1О1В1: Отсюда: 2). 3). Следствие. Площади подобных многоугольников относятся как квадраты радиусов описанных окружностей или как квадраты радиусов вписанных окружностей. Билет № 7. Теорема Фалеса. Свойство средней линии треугольника. Доказать. Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные между собой отрезки и на другой его стороне.
A1B1 II A2B2 II A3B3; A1A2 = A2A3. Доказать: В1В2 = В2В3. Доказательство: 1. Дополнительное построение: Через точку В2 проведем прямую FE II OA, такую, что  2. Полученные четырехугольники FA1A2B2 и ЕA3A2B2 являются параллелограммами по определению (противоположные стороны попарно параллельны). По свойству параллелограмма: 3. Рассмотрим ∆ FB1B2 и ∆В2B3Е. 4. Из ∆ FB1B2 = ∆В2B3Е Þ B1B2 = В2B3. Замечание: В условии теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключение теоремы будет то же.
Обратная теорема Фалеса. Если на одной стороне угла от его вершины отложены равные отрезки ОА1, A1А2, A2А3, ... и на другой его стороне также отложены соответственно равные отрезки ОВ1, В1B2, B2В3,то прямые A1В1, А2B2, ... параллельны. Дано: ÐAOB; B1B2 =В2B3=…; A1A2 = A2A3=…. Доказать: А1В1 II A2В2…. Доказательство: 1. DOA1B1~ DOA2B2 (по пропорциональным сторонам и углу между ними).
ÐO-общий. 2. Из подобия треугольников следует: ÐOA1B1 = Ð OA2B2 – соответственные Þ A1B1 II A2B2. Аналогично доказывается параллельность других прямых. Определение 1. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Свойство средней линии треугольника. Средняя линия треугольника параллельна основанию треугольника и равна его половине.
Дано: DABC; MN, ND, MD – средние линии. Доказать: MN II AC; Доказательство: 1. Продолжим MN за точку N и на продолжении отложим PN = MN. 2. Рассмотрим DMBN и DNPC. BN = NC (по определению средней линии); MN = NP (по построению); ÐMNВ = ÐPNC (вертикальные); Þ DMВN = DNPC (по 1 признаку). 3. ÐBMN = ÐNPC (внутренние накрест лежащие) Þ АВ II PC. 4. CP = MB (из равенства треугольников); AM = MB (по определению средней линии); Þ CP = АM. 5. АM II PC; AM = PC Þ AMPC – параллелограмм Þ AC = MP; AC II MP. 6. MP = 2MN (по построению) Þ MN = 0,5AC. 7. AC II MP; MNÌMP; Þ MN II AC.
Доказать теорему о площади трапеции. Следствие. Доказать, что длина отрезка, параллельного основаниям трапеции и делящего трапецию на две равновеликих трапеции, равна среднему квадратичному оснований. Определение 1. Высотой трапеции называется общий перпендикуляр ее оснований (или прямых, содержащих основания). Теорема о площади трапеции. Площадь трапеции равна произведению полусуммы оснований и высоты: Доказательство:
Следствие из теоремы о площади трапеции. Площадь трапеции равна произве Доказательство:
По свойству средней линии трапеции
Доказательство: 1. Пусть AD = a, BC = b, BE = h. 2. По свойству равновеликости площадей: 3. По свойству равносоставленности площадей: Билет № 8. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 278. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 и т. д.
и т. д.

 Дано: ÐAOB;
Дано: ÐAOB; 
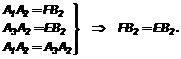

 Обобщенная теорема Фалеса. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные между собой отрезки и на другой прямой.
Обобщенная теорема Фалеса. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные между собой отрезки и на другой прямой. OA2 = OA1 + A1A2 = 2OA1; OB2 = OB1 + B1B2 = 2OB1.
OA2 = OA1 + A1A2 = 2OA1; OB2 = OB1 + B1B2 = 2OB1. 




 дению средней линии и высоты:
дению средней линии и высоты: 

 Поэтому
Поэтому 
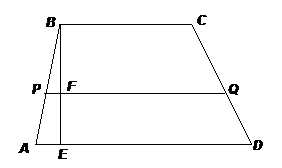 Теорема 2. Длина отрезка, параллельного основаниям трапеции и делящего трапецию на две равновеликие трапеции, равна среднему квадратичному оснований:
Теорема 2. Длина отрезка, параллельного основаниям трапеции и делящего трапецию на две равновеликие трапеции, равна среднему квадратичному оснований: 

