
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение 2. Многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник, если все стороны многоугольника являются касательными к окружности.В многоугольник можно вписать окружность, если найдется точка, равноудаленная от всех его сторон. Эта точка лежит на биссектрисе каждого угла многоугольника. Следовательно, в многоугольник можно вписать окружность тогда и только тогда, когда биссектрисы всех его углов имеют общую точку. Эта точка и будет центром вписанной окружности. Теорема 2: В любой правильный многоугольник можно вписать окружность, и притом только одну.
Дано: А1А2…Аn – правильный многоугольник. Доказать: 1) существует окружность с центром О, вписанная в многоугольник А1А2…Аn; 2) эта окружность единственная. Доказательство: 1) Из доказательства предыдущей теоремы следует, что серединные перпендикуляры 2) Докажем, что эта вписанная окружность единственная. Предположим, что наряду с рассматриваемой окружностью с центром в точке О и радиусом ОN1 существует и другая вписанная в многоугольник окружность с центром в точке О1. Тогда точка О1 равноудалена от сторон многоугольника и лежит на каждой из биссектрис его углов, а следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. равен ОN1. Таким образом, вторая окружность совпадает с первой. Теорема доказана. Следствие 1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Следствие 2. Центр окружности, описанной около правильного многоугольника, совладает с центром окружности, вписанной в этот многоугольник. Эта точка называется центром правильного многоугольника. 
Билет № 5. Параллелограмм. Свойство углов и сторон параллелограмма. Признаки параллелограмма. Определение 1. Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом. У каждого параллелограмма четыре вершины, четыре стороны, четыре угла. Две стороны, имеющие общие концы, называются смежными. У каждого параллелограмма две диагонали – отрезки, соединяющие противоположные вершины параллелограмма. Сумма углов параллелограмма равна 360°. Свойства параллелограмма.
Доказательство: Проведем диагональ АС. АС – общая; ÐВАС = ÐАСD (внутренние накрест лежащие при АВ II BC и секущей АС); ÐВСА = ÐСАD (внутренние накрест лежащие при АD II BC и секущей АС); Þ DАВС = DАDС (по 2 признаку). АВ = CD; BC = AD; ÐВ = ÐD. ÐА = ÐВАС + ÐСAD; ÐС = ÐАСB + ÐАСD; Þ ÐА = ÐС. Свойство 2. У параллелограмма углы, прилежащие к одной стороне, в сумме дают 180°. Доказательство: ÐВ + ÐА =180° (внутренние односторонние при ВС II AD и секущей АB). ÐB + ÐС =180° (внутренние односторонние при AВ II CD и секущей BC). ÐD + ÐC =180° (внутренние односторонние при ВС II AD и секущей CD).
Свойство 3. Диагонали параллелограмма точкой пересечения делятся пополам. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 294. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
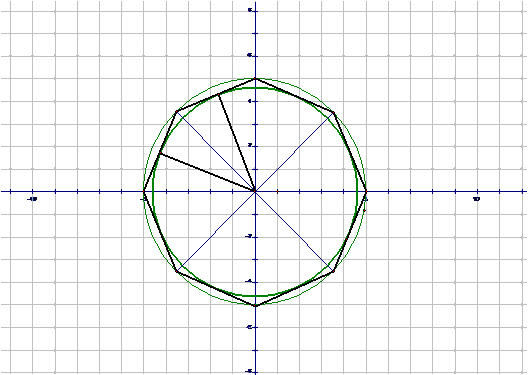
 Таким образом, окружность радиуса ОN1 c центром в точке О является вписанной в многоугольник А1А2…Аn окружностью.
Таким образом, окружность радиуса ОN1 c центром в точке О является вписанной в многоугольник А1А2…Аn окружностью. 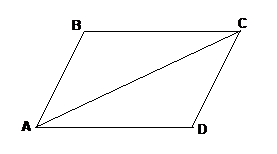 Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны.
Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны. ÐA + ÐD =180° (внутренние односторонние при AВ II CD и секущей AD).
ÐA + ÐD =180° (внутренние односторонние при AВ II CD и секущей AD).