Існування 5 типів правильних многогранників. Топологічна класифікація многогранників

Назвемо простий многогранник топологічно правильним, якщо всі його грані мають одне і теж число вершин, а всі многогранні кути – одне і теж число граней. Нехай F –топологічно правильний многогранник. Позначимо через n число вершин кожної грані, через g – число граней кожного його многогранного кута, а через відповідно число вершин, ребер і граней. Кожне ребро многогранника F є спільною стороною дох його граней, а кожна грань містить n ребер. Тому  (1)Кожна вершина многогранника F є спільним кінцем g ребер. Отже (2). Оскільки Підставивши сюди значення із (1) і (2) отримаємо (3) Звідси випливає  (4)

Так як  і  , то з нерівності(4) отримаємо  , тому g<6. Аналогічно отримаємо n<6. Таким чином

Тобто g і n можуть приймати тільки значень 3, 4, 5 Із нерівності слідує, що числа одачасно не можуть бути >3, тобто хоча б одне з них = 3.Отже можливі такі комбінації: 1) g=n=3, 2)g=3,n=4 3)g=3, n=5; 4)g=4,n=3; 5)g=5, n=3. В кожному з випадків ми можемо знайти

Отже, будь-який топологічно правильний многоранник належить одному з наступних типів

№	Назва	g	n
1	Тетраедр	3	3	4	6	4
2	Гексаедер	3	4	8	12	6
3	Додекаедер	3	5	20	30	12
4	Октаедер	4	3	6	12	8
5	Ікосаедер	5	3	12	30	20

Ми довели, що існує не більше 5 типів топологічно правильних многоранників

1. 1.Куб. Разг. тригранний кут з вершиною О, ребра якого взаємно перпендик. Від точки О на ребра цього тригранного кута відкладемо відрізки ОА, ОВ, ОС і через кожну з точок проведемо площини паралельні грані, яка проходить через інші точки. Отримаємо випуклий многогранник.Його гранями є 6 рівних квадратів -> тому він наз. Правильним гексаедром або кубом

2. Правильний тетраедр.Нехай ABCDA1B1C1D1 –куб. Точки A, B1, C, D1 не лежать в одній площині, тому є вершинами якогось тетраедра Т. Поверхня цього тетраедра утворена 4-а рівними правильними трикутниками ,т.я. сторони цих трикутників є діагоналями граней куба. Многогранні кути при вершинах тетраедра Т мають одне і теж число граней(3).--> T- правильний тетраедр

3.Правильний октаедр. Побудувавши три рівних попарно перпендикулярних відрізки AA', BB’, CC’, які мають спільну середину О.                           A,B,C,A’,B’,C’ є вершинами правильного восьмигранника, гранями якого є рівні друг другу правильні трикутники ABC, ABC’ ,BA’C, BA’C’, A’B’C, A’B’C’, B’AC, B’AC’. Цей многогранник наз правильним октаедром. О рівновіддалена від всіх верших, граней і ребер правильного октаедра тому О – центр правильно октаедра

4. Правильний ісокаедр. Будуємо три рівні попарно перпендикулярних відрізки     AA', BB’, CC’, які мають спільну середину О. Позначимо через 2а довжиу кожного відрізку. Потім побудуємо рівні відрізки  і     з серединами в точках А і А’ паралельні ВВ’. Позначимо довжини 2b. Будуємо відрізки              і з серединами у точках В і В’, паралельних CC’і рівних 2b.Аналогічно 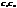 і 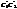 паралельних АА’ і =2b.Отримаємо , які є вершинами правильного ікосаедра. Побудуемо грані. Розглянемо площину АОВ. ,  і відрізок лежать по одну сторону від АОВ, а    по іншу. Зєднав кінці відрізка  з точками  , , а з і 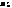 отримаемо 4 рівнобедрених трикутники 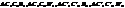. Розглянув АОС отримаемо .Розгл ВОС отримаємо . Ми отримаемо 12 рівнобедрених і ще 8 правильних трикутників. a і b можна підібрати так, щоб отриманий многогранник був правильним.

5. Правильний додекаедр.Центри граней правильного ікосаедра слугують вершинами правильного додекаедра