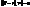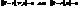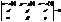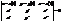Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Різні види рівняння кривої у просторі. Тригранник Френе.Відображ. фігури F у фігуру F’ наз. неперерв., якщо воно близькі точки фігури F перевод. у близькі точки фігури F’. Відображ. f фігури F у фігуру F’наз. топологічним(гомеоморфним), якщо воно бієктивне і взаємно неперервне. Відображ. фігури наз. локально-топологічним, якщо воно є гомеоморфним в околі кожної її точки. Множина γ точок простору наз. елементарною кривою, якщо ця множина є образом відкритого відрізка прямої при його топологіч. відображ. в просторі. Простою кривою наз. фігура, кожна точка якої має такий просторовий окіл, що частина фігури, яка міст. в цьому околі, є елемент. кривою. Загальною кривою наз. фігуру, що одерж. локально топологіч. відображ. простої кривої, тобто таку криву можна покрити закінч. або зчислен. множ. елемент. кривих. Нехай у прямокут. репері
(1) – параметрич. р-ня кривої
Дві параметриз Якщо лінію можна задати р-ням: У цьому випад. лінія є перетином 2-х циліндрів.
Пряму наз. регулярною класу Ck, де k≥1 (k раз диференційовано), якщо вона допускає регулярну параметриз., тобто задання її параметрич. р-нями (1)
lv - головна нормаль lβ - бінормаль  lτ - дотична
На кожній з прямих тригран. вказ. одиничний вектор: v – одинич. вектор дотичної β - одинич. вектор головної нормалі τ - одинич. вектор бінормалі
В кожній точці кривої
Рівняння елементів тригран. Френе: Дотична
Бінормаль
Головна нормаль
Нормальна площина
Спрям на площина
Стична площина
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 601. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
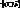
 - елемент. крива, яка є тополог. образом відрізка АВ. Якщо на прямій АВ як числовій осі ввести координату t, то відображ. відрізка АВ в криву γ можна задати р-нями:
- елемент. крива, яка є тополог. образом відрізка АВ. Якщо на прямій АВ як числовій осі ввести координату t, то відображ. відрізка АВ в криву γ можна задати р-нями: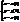 (1), де x(t), y(t), z(t)неперер. ф-ії
(1), де x(t), y(t), z(t)неперер. ф-ії (2) векторне р-ня кривої
(2) векторне р-ня кривої наз. еквівалентними, якщо існує допустима заміна параметра t=t(u):
наз. еквівалентними, якщо існує допустима заміна параметра t=t(u): 
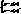 явне (канонічне) задання кривої.
явне (канонічне) задання кривої.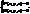 неявне задання кривої.Перетин будь-яких 2-х поверхонь.
неявне задання кривої.Перетин будь-яких 2-х поверхонь.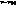 наз. натуральною параметризацією, де
наз. натуральною параметризацією, де 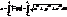
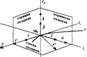 В кожній точці регул. прямої класу C2 існує так званний тригранник Френе.
В кожній точці регул. прямої класу C2 існує так званний тригранник Френе.

 визнач. стичну площину, lv, що лежить в стичній площині і перпендик. до дотичної lτ наз. головною нормалю кривої. lβ, що проход. ч/з т.М0 і перпендик. до стичної площини наз. бінормаллю.lβ іlvперпендик. до дотичної визнач.нормальну площину.Дотична і нормаль визнач. спрямну площину.
визнач. стичну площину, lv, що лежить в стичній площині і перпендик. до дотичної lτ наз. головною нормалю кривої. lβ, що проход. ч/з т.М0 і перпендик. до стичної площини наз. бінормаллю.lβ іlvперпендик. до дотичної визнач.нормальну площину.Дотична і нормаль визнач. спрямну площину. тригранник Френе, який визнач. 3-ма площинами, які попарно перетин. по 3-м прямим, при цьому в кожній точці кривої існує прямо кут. декартовий базис, за базисні вектори беремо (τ, v, β)
тригранник Френе, який визнач. 3-ма площинами, які попарно перетин. по 3-м прямим, при цьому в кожній точці кривої існує прямо кут. декартовий базис, за базисні вектори беремо (τ, v, β)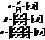
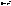 напрямлений вектор =
напрямлений вектор = 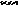
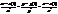 канонічне рівняння
канонічне рівняння
 -напрямлений вектор =
-напрямлений вектор = 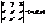
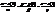 канонічне рівняння
канонічне рівняння
 -напрямлений вектор =
-напрямлений вектор = 
 канонічне рівняння
канонічне рівняння