
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Група афінних перетворень площини і її підгрупи.Афінне перетвор.– це перетвор.площини, яке перевод. 3 точки Афінне перетвор. можна задати ф-ми: Доведемо, що множина афінних перетвор.А утворює групу. Доведемо, що якщо Доведемо, якщо Група Р подібностей площини є підгрупою групи А, група D рухів є підгрупою групи А. Іншими підгрупами є: а) сукупність 
Начала» Евкліді. Проблема 5-го постулату. Огляд аксіоматики гільберта евклідової геометрії. «Начала», яка розбивалась на 13 книг: 1)виклад теорії Δ-ків, | | прямих, умови рівно великості Δ-ків, мн-ків, теорема Піфагора; 2)Перетворення мн-ка в рівновеликий квадрат (алг. тотожність в геом.. формі); 3)Відомості про коло; 4)Вписані і описані мн-ки, побудова пр.n-кутників; 5)Теорія пропорцій; 6)Подібність мн-ків; 7, 8, 9) Арифметика в геом.. викладі. Т. про нескінч. мн-ни простих ч-л; 10) невимірні величини, теорія квадр. ірац.; 11, 12, 13) Основи стереометрії. Постулати: 1.2 точки визн. пряму лінію; 2.Кожну необм. пряму можна необм. продовжити; 3.З любого центра можна описати коло 4.всі прямі кути рівні між собою; 5.Якщо при перетині 2-х Аксіоми: 1.Рівні окремо 3-му, рівні між собою. 2.Якщо до рівних додати рівні, то одерж. рівні. 5.Всяке ціле > частини. 7. Ті, що суміщаються, рівні між собою. «Начала» мають недоліки: 1)озн-ня фіктивні, не використ.; 2)перелік постулатів є неповним; 3)при д-ні т-м посилання на наочні зображ.; 4)пит-ня неперервності прямої та кола не обгрунт.; 5)теорія вимірювання довжин не була викладена по суті. Проблема V-го постулату. Проблема: Пробували д-ти як т-му. В 1-й книзі 28 т-м д-ся без використання V-го постулату. Евклід д-ть, що 2 Відомі д-ня V-го постулату: Перокл, Омар Хайям, Вайліс,. Це д-ня хибні, всі автори опирались на деякі твердж., які еквівалентні V-му постулату. Аксіоматика Гілберта.Виділяє 3 типи геом. об’єктів: 1) точки; 2) прямі; 3) пл.-ни. Осн. неозн. відн-ня: 1) інцендентність (належність); 2) лежати «між» для 3-х т-к;; 3) конгруентність для кутів і відрізків. Всього аксіом 20, розбиті на 5 груп: 1) аксіоми інцендентності; 2) аксіоми порядку (4); 3)аксіоми конгруентності; 4) аксіоми неперервності; 5) аксіоми ||-ті. 1. Аксіоми належності та наслідки з них : 1.1. для 1.2. Для З цих 2-х аксіом 1.3. для З 1-3 1.4. для 1.5. Для 1.6. Якщо 2 т-ки 1.7. Якщо для 2 пл-н α і β 1.8. 2. Аксіоми порядку і деякі наслідки: 2.1. якщо т.В лежить між А і С, то А,В,С – 3 різні т-ки 1-ї прямої, і В лежить між А і С. 2.2. Для 2.3. із 3 т-к, що Т-ма:
3. Аксіоми конгруентності.1. нехай А і В – 2 різні т-ки прямої а і мають т-ку А1, інц. а1, тоді 2. якщо відрізок [А1В1] конгр. [АВ] і [А2В2] конгр.[АВ] 3. Якщо В лежить між А і С і В1 лежить між А1 і С1 і [А1В1] конгр.[АВ]і [В1С1] конгр.[ВС] 4. В заданій півпл-ні і заданим на ній променям можна побудувати кут конгр. заданому і тільки !. 5. якщо для ΔАВС і ΔА1В1С1 викон. умови: АВ конгр. А1В1, АС конгр. А1С1 і < BAC конгр.< B1A1C1. 4. Аксіоми неперервності. 4.1. аксіома Архімеда – нехай маємо 2 в-ки Ав і СD, тоді на прямій АВ 1)А1А^2А3, А2А^3А4,…,Аn—2 A ^n-1 A n 2) [A1A2]конгр. [A2A3]… [An-1An]; 3) AB^An. Змістовно: Малим відрізком СD можна перекрити 4.2. Аксіома Кантора. Нехай на деякій прямій задана нескінч. к-ть від-ків А1В1, А2В2,…,АnBn, такі що кожний леж. В середині. Нехай для Аксіома Дедекінда. Нехай задано розбиття т-к АВ на 2 класи. Клас К1і К2, такі що К1 К1 Т-ка М0 буде або ост. Т-кою 1-го класу, або першою 2-го класу. Аксіом довжин в-ка(3): 1) Т. Якщо при перетині 2 прямих а і b 3 с, внутр. різностор.кути конгр., то ці 2 прямі а і b ||. Д-ня. Припустимо, що вони Т. Є пряма а і т-ка А поза прямою ч\з А можна провести принаймні 1-ну пряму, яка буде || а. д-ня.скорист. попередн. Т-мою. На основі аксіом 3-4(конгр. для кутів) по від-ню до променя АВ |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 575. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
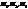 , що належ. одній прямій, в три точки
, що належ. одній прямій, в три точки 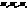 , що лежать на одній прямій і при цьому зберіг. їх просте віднош.. Будь-яке перетвор. подібності – це афінне перетвор. оскільки при ньому пряма переход. в пряму і зберігається віднош. точок. Тому будь-який рух є афінним перетвор. Афінне перетвор. пряму переводить в пряму, || прямі в ||прямі, півплощини в півплощини, промінь в промінь, відрізок у відрізок, кут в кут. Якщо точки А,В,С не належ.одній прямій, вони є нерухом. точками афінного перетвор.
, що лежать на одній прямій і при цьому зберіг. їх просте віднош.. Будь-яке перетвор. подібності – це афінне перетвор. оскільки при ньому пряма переход. в пряму і зберігається віднош. точок. Тому будь-який рух є афінним перетвор. Афінне перетвор. пряму переводить в пряму, || прямі в ||прямі, півплощини в півплощини, промінь в промінь, відрізок у відрізок, кут в кут. Якщо точки А,В,С не належ.одній прямій, вони є нерухом. точками афінного перетвор.  , то
, то 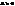 ;2 роду – змінює,
;2 роду – змінює, 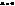 .
.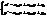
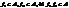 . Дійсно, оскільки
. Дійсно, оскільки  і
і  перетвор., то
перетвор., то 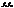 - перетвор.. Але кожне з перетвор.
- перетвор.. Але кожне з перетвор. 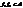 .
.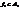 то
то 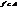 . Дійсно, якщо точки А,В,С лежать на одній прямій то їх образи
. Дійсно, якщо точки А,В,С лежать на одній прямій то їх образи 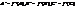 також належ. одній прямій, оскільки, якщо припустити обернене, то знайдет. такий репер
також належ. одній прямій, оскільки, якщо припустити обернене, то знайдет. такий репер  , який в перетвор. переходить в 3 точки А,В,С, які належ.ь одній прямій, що неможливо. Тому
, який в перетвор. переходить в 3 точки А,В,С, які належ.ь одній прямій, що неможливо. Тому  зберігає просте віднош. 3 точок.
зберігає просте віднош. 3 точок.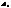 всіх афінних перетворень 1 роду; б) сукупність
всіх афінних перетворень 1 роду; б) сукупність 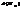 всіх афінних перетворень, для яких
всіх афінних перетворень, для яких 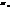 - нерухома точка(група центро-афінних перетворень); в)сукупність
- нерухома точка(група центро-афінних перетворень); в)сукупність  всіх афінних перетворень, для яких пряма
всіх афінних перетворень, для яких пряма  складається з нерухомих точок.
складається з нерухомих точок. радіуса;
радіуса; прямі до однієї прямої не
прямі до однієї прямої не  , а значить є ||. Якщо має місце, що ч\з т-ку можна провести пряму, то V-й постулат діє.
, а значить є ||. Якщо має місце, що ч\з т-ку можна провести пряму, то V-й постулат діє. пряма, така, що А
пряма, така, що А  а і В
а і В  наслідок: для 2-х різних т-к
наслідок: для 2-х різних т-к  одній прямій,
одній прямій,  із 3 т-к 1-на і тільки 1-на лежить між2 ін. Відрізок має нескінч. мн-ну внутр. т-к
із 3 т-к 1-на і тільки 1-на лежить між2 ін. Відрізок має нескінч. мн-ну внутр. т-к  К2 = [AB]
К2 = [AB] <AK || a.
<AK || a.