Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кривина та скрут просторової кривої. Формули Френе.Якщо крива Кривина кривої Якщо крива задана параметрич. р-нями Зокрема, якщо в ролі параметра кривої вибраний натур. параметр s, то Точки в яких k = 0, наз. точками розпрямлення. Ця назва виправдана такою властив.: для того, щоб крива γ була прямою лінією, необх. і досить, щоб у кожній її точці k = 0. Величина Якщо крива, Скрут кривої, заданої р-ням У випад. натур. параметриз. кривої, тобто Рівність нулю скрута кривої у всіх точках є необх. і достат. умовою того, щоб крива була плоскою. Точки, в яких χ = 0, наз. точками сплощення кривої. Як виплив. із ф-ул для визнач χ,в точках розпрямлен. кривої (тобто в точках, де k = 0) скрут невизначю ТеорФрене: похідні від базисних векторів в локальній системі координат є лінійними комбінаціями цих базисних векторів.
Вивід формул Френе: 1) 2) 3).
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 575. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , то визнач. її кривина k – модуль швидкості обертання дотичної по віднош. до довжини дуги:
, то визнач. її кривина k – модуль швидкості обертання дотичної по віднош. до довжини дуги:  .
.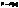 обчисл. за ф-лою
обчисл. за ф-лою  . (1)
. (1) то
то  (2)
(2) , а в корд.
, а в корд.  . (3)
. (3) наз. радіусом кривини кривої. Якщо від т.М кривої на голов. нормалі в додат. напрямку відклас. відрізок довжиною R, тот одержана т.C носить назву центра кривини кривої, що відпов. т.М.
наз. радіусом кривини кривої. Якщо від т.М кривої на голов. нормалі в додат. напрямку відклас. відрізок довжиною R, тот одержана т.C носить назву центра кривини кривої, що відпов. т.М. , то скрут χ цієї кривої (без урахування знаку) – це швидкість обертання стичної площини навколо дотичної або, що те саме, швид. зміни напряму бінормалі:
, то скрут χ цієї кривої (без урахування знаку) – це швидкість обертання стичної площини навколо дотичної або, що те саме, швид. зміни напряму бінормалі:  .
.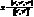 (4) або в корд. вигляді
(4) або в корд. вигляді 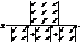 (5)
(5) , то
, то  (6) або
(6) або  (7)
(7) ,
,  ,
,  - формули Френе
- формули Френе ;
;  - залежать від
- залежать від  .
.