Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Поверхні в евклідовому просторі. Криволінійні координати на поверхні. Дотична площина і нормаль поверхні.Під елементарною поверхнею розуміють множину точок простору (фігуру), гомеоморфну відкритій плоскій області. Проста поверхня - це фігура, в околі кожної точки якої вона є елементар. поверхнею. Загальна поверхня - це фігура, яка одерж. локально-топологічним перетвор. простої поверхні. Основою вивчення поверхні є елементарна поверхня. Якщо в площині D ввести афінні координати и, v, а в просторі Ез – прямо кут. с-му коор. Р-ня Числа u і v повністю характериз. положення т.M на поверхні і наз. внутрішніми, криволінійними або гаусовими координатами на поверхні. Перейшов. до коор. в базисі Поверхня наз. регулярною класу Сk (k≥1), якщо вона допус. регулярну параметриз., тобто задання р-нями (2) в параметрич. формі, де x(u,v), y(u,v), z(u,v) - k раз неперервні диферент. ф-ії, що задовол. умові У випад. вектор. задания поверхні ця умова означ., що Рівняння виду: Очевидно, що від р-ня (3) легко перейти до параметрич., поклавши x=u,y=v В остан. р-ні роль кринолін. координат u , v відіграють х, у. У вектор. формі це р-ня приймає вигляд Всі точки поверхні, задан. р-ням (3), звичайні, адже Неявне р-ня поверхні має вигляд F(x, y, z) = 0, (4), де функція F належить класу Ck (k≥1). P-ня u-лінії має вигляд Будь-яку криву на поверхні можна задати в криволін. с-мі коор. u, v за допом. параметрич. р-нь  Векторне р-ня такої кривої матиме вигляд Р-нями дотич. площини, що відповід. річним способам задання поверхні відпов. будуть:
Нормаллю до поверхні в т.M наз. пряма, що проход. ч/з цю точку перпендик. до дотичної площини. Очевидно, що вектор Якщо поверхня задана неявним р-ням F(x,y,z) = 0, то Нормалі задаються такими рівняннями:
19. Перша та друга квадратичні форми поверхні та їх застосування. Нехай регулярна поверхня задана р-ням
де Квадратич.форма І наз. першою квадратич. формоюповерхні або лінійним елементом поверхні Вона = квадрату диференціала дуги будь-якої кривої, яка проходить через задану т.M(u,v), напрям якої визнач. диференціалами du, dv. Перша квадратична форма завжди додатньовизначена. Якщо поверхня задана явним рівнянням z=z(x,y), то, вибравши в ролі кринолін. коор. змінні х,у, легко перейти до параметрич.р-нь х=х, у=у, z=z(x,y). Тоді
Застосування. 1. Довж. дуги плоскої лінії (**), розташов. на поверхні (*), обчисл. за ф-ою
Для знаходження довж. кривої на поверхні досить знайти її першу квадратич. форму. У зв'язку з цим кажуть, що І квадратич. форма поверхні задає її метрику. 2. Кут між двома кривими. Нехай на поверхні задані 2 криві γ1 і γ2, які перетин. в т.М. Нехай дотичні до них визнач. векторами Кут θ між кривими - це кут між напрямними векторами du і
Звідки
3. Площа σ замкненої обл. D поверхні обчисл. так
Якщо поверхня задана явним р-ням z=z(x,y), то Сукупність властив. поверхні, які можна вираз. ч/з коефіц. її першої квадрат. форми наз. внутріш. геомет. поверхні. Деформація поверхні, при якій вона не розтяг., не стиск., не розрив. і не склеюєт., наз. зганянням поверхні Оскільки при такій деформації зберіг. довжини всіх дуг на поверхні, отже, і диференціали цих дуг, то зберігатиметься і перша квадрат. форма. Тобто при згинанні поверхні зберіг. її внутр. геом., хоч просторова форма змін. Таким чином, перша квадрат. форма поверхні визнач. її з точністю до згинання. Для однознач. визнач. поверхні як жорсткого тіла, тобто визнач. її з точністю до руху, потрібно задати для неї ще і так звану другу квадратичну форму
а Якщо поверхня задана в явному вигл. z=z(x,y), то
Кривина похилого перерізу: Якщо в ролі кривої на поверхні вибрати переріз площиною, перпендик. до дотичної площини (так званий нормальний переріз), то тобто на відміну від k нормальна кривина ки може бути і від'ємною, а саме |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 578. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
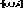 , то радіус-вектор
, то радіус-вектор  є векторною ф-єю 2х змінних u, v.
є векторною ф-єю 2х змінних u, v.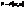 (1) наз. векторним р-ням поверхні.
(1) наз. векторним р-ням поверхні.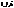 вектор. р-ні (1), одержимо параметрич. р-ня поверхні
вектор. р-ні (1), одержимо параметрич. р-ня поверхні 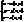 (2)
(2)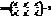
 не колінеарний
не колінеарний  . При k=1 поверхня наз. гладкою.
. При k=1 поверхня наз. гладкою.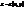 наз. явним р-ням поверхні.
наз. явним р-ням поверхні.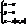 або
або 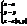
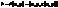 (3)
(3)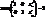 , тобто
, тобто  не колінеарний
не колінеарний 
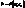 ,а v-ліиії-
,а v-ліиії- 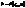 . Тоді
. Тоді 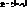 - є вектор, дотичн. до координатної u-лінії, а
- є вектор, дотичн. до координатної u-лінії, а 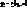 – дотичн. до v-лінії, при цьому
– дотичн. до v-лінії, при цьому  не колінеарний
не колінеарний 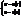 (*)
(*)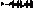 . Нехай M(u,v) - точка поверхні, а (*) - будь-яка крива, що проход. ч/з цю точку. Напрям дотичної до цієї кривої визнач. вектором
. Нехай M(u,v) - точка поверхні, а (*) - будь-яка крива, що проход. ч/з цю точку. Напрям дотичної до цієї кривої визнач. вектором 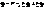 . Для різних кривих, що проход. ч/з т.М, ф-ії
. Для різних кривих, що проход. ч/з т.М, ф-ії  і
і  будуть різні, а
будуть різні, а  є лінійн. комбінац. векторів
є лінійн. комбінац. векторів 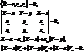
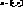 буде напрямним вектором нормалі та нормальним вектором дотичної площини.
буде напрямним вектором нормалі та нормальним вектором дотичної площини.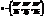
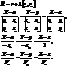
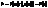 . При цьому
. При цьому 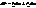 , де
, де 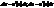 . Для кривої
. Для кривої 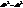 - де ds - диференціал довжини дуги кривої. Підставивши в останню рівність знач.
- де ds - диференціал довжини дуги кривої. Підставивши в останню рівність знач.  , маємо
, маємо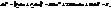 (1)
(1)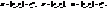
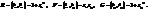 , а
, а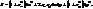 (2)
(2)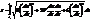 .
.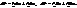
 їх дотич., отже
їх дотич., отже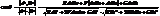 (4)
(4)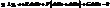 . Для u-лінії du≠0, dv=0. Для v-лінії
. Для u-лінії du≠0, dv=0. Для v-лінії  =0.
=0. 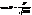 (5) Звідки координатна сітка (u, v) на поверхні ортогональна ↔коли F=0.
(5) Звідки координатна сітка (u, v) на поверхні ортогональна ↔коли F=0.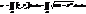 (6)
(6)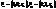 . Тоді
. Тоді 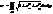
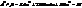 , де
, де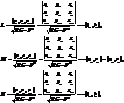
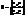 - одиничний вектор нормалі до поверхні.
- одиничний вектор нормалі до поверхні.
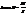 де θ – кут між вектором
де θ – кут між вектором  і площиною похилого перерізу поверхні.
і площиною похилого перерізу поверхні.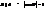 , а значить кривина нормального перерізу поверхні
, а значить кривина нормального перерізу поверхні 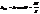 , (3)
, (3)