
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Зависимость теплового эффекта от температурыЕсли внутренняя энергия является функцией температуры, то тепловой эффект процесса с ней непосредственно связанный тоже будет зависеть от температуры. С тепловым эффектом связана теплоемкость системы:
Полученные дифференциальные уравнения называются уравнениями Кирхгофа. Из уравнений Кирхгофа следует, что температурный коэффициент процесса (химической реакции, фазового перехода и др.) равен изменению теплоемкости в результате протекания этого процесса. После интегрирования уравнения Кирхгофа, принимая Р = const:
где На практике нижним пределом такого температурного интервала как правило является 25°С (298 K). В этом случае уравнение преобразуется к виду:
Расчет количества теплоты Закон Гесса используют при вычислении общего количества теплоты, необходимого для нагревания (или выделяющегося при охлаждении) любой системы от Тi до Тk при Р = соnst. Частный случай 1 – нагревание вещества от обычной температуры до заданной без фазового превращения:
Частный случай 2 – нагревание вещества от обычной температуры до заданной с фазовым превращением:
Данные, необходимые для расчетов приводятся в справочниках термодинамических величин. При приближенных расчетах можно пользоваться стандартными величинами теплоемкости Понятие об энтропии Процессы можно разделить на две группы – самопроизвольные и не самопроизвольные. Самопроизвольные процессы протекают без участия внешней энергии. Определение возможности и условий самопроизвольного протекания процесса входит в основные задачи термодинамики.  Рассмотрим следующую ситуацию. Системе с исходным уровнем энергии i сообщено некоторое количество энергии в виде теплоты. Передача теплоты происходит за счет увеличения кинетической энергии теплового движения частиц. Ограничим систему условием постоянства объема. В ответ система выполнила работу и перешла в состояние равновесия k. Изменение внутренней энергии:
Часть энергии пошла на совершение системой работы, а часть – на увеличение энергии хаотического теплового движения частиц. Теплота полностью в полезную работу не перешла (Uk > Ui). Отсюда формулировка второго закона термодинамики: вся теплота не может быть превращена в работу. Доля энергии, которая в работу не переходит, а рассеивается на броуновское движение, должна зависеть от свойств системы: агрегатного состояния, строения вещества, т.е. от тех свойств системы, которые определяют степень хаотичности теплового движения частиц. Количественная мера рассеиваемой энергии должна быть функцией состояния системы и ее однозначной характеристикой. Такая функция для равновесного обратимого процесса определяется уравнением
является количественной характеристикой рассеяния энергии или энтропией. При протекании процесса необратимого
Получается, что изменение энтропии – мера необратимости процесса. Чем выше энтропия системы, тем больше теплоты не переходит в полезную работу, тем больше необратимость процесса. Для изолированных систем однозначно самопроизвольно протекают процессы, сопровождающиеся ростом энтропии. При состоянии равновесия величина энтропии не меняется. Фазовые превращения протекают при Р, Т = const. В связи с этим для вычисления изменения энтропии можно использовать уравнение
При изменении давления в системе изменение энтропии определяется уравнением
В силу того, что энтропия – функция состояния, то к ней применим закон Гесса:
где ν – стехиометрический коэффициент; индекс i относится к исходным веществам, индекс k – к продуктам реакции. Зависимость изменения энтропии химической реакции от температуры описывается уравнением:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 580. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
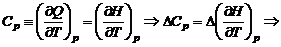
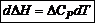
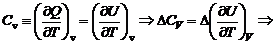
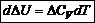
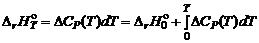 ,
,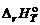 – тепловой эффект при заданной температуре,
– тепловой эффект при заданной температуре, 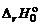 – тепловой эффект процесса при 0 K.
– тепловой эффект процесса при 0 K.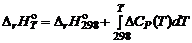
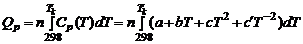
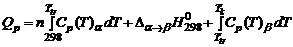
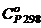 /
/
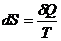 ,
,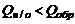 , следовательно
, следовательно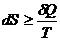 или
или 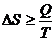 - в общем случае.
- в общем случае.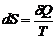 или
или 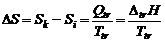
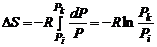 .
.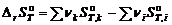 ,
,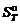 – энтропия образования вещества, приведенная к стандартным условиям при температуре Т.
– энтропия образования вещества, приведенная к стандартным условиям при температуре Т.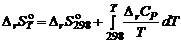 .
.