Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Мощность в цепях синусоидального тока
Как известно, мощность в электрических цепях формируется законом Джоуля-Ленца и всегда сопровождается выделением тепла. Закон Джоуля-Ленца применительно к цепям переменного тока имеет вид:
Здесь Р – мощность на участке электрической цепи, I – среднеквадратичное (действующее) значение тока в нем, а R – активное сопротивление участка. Простые математические преобразования приводят эту формулировку закона к виду:
где U – среднеквадратичное значение напряжения на участке, а g – его активная проводимость. Любой участок электрической цепи синусоидального тока как обобщенный приемник электрической энергии может быть в полной мере описан подобными друг другу треугольниками напряжений, токов, сопротивлений и проводимостей. Если все стороны треугольника сопротивлений участка цепи умножить на квадрат действующего значения тока в нем, получаем треугольник, который называется треугольником мощностей (см. рис. 2.32).
Рис. 2.32
С принципиальной точки зрения здесь мощность только одна, представляемая прилежащим к углу j катетом, величина которого Имеющая размерность мощности величина противолежащего катета При x = xL – xC получаем:
что в цепи формально можно рассматривать как наличие отдельно индуктивной  Реактивная мощность, формально не являясь таковой, никакой работы в цепи не производит, имеет размерность «Вольт-Ампер» [А2×Ом = В×А], называемую «ВАр» (вольт-ампер-реактивный). Величина гипотенузы треугольника Из треугольника мощностей получаем:
Если активная мощность не изменяет своего знака и однонаправлено удаляется из цепи в виде тепла, реактивная мощность может быть и положительной (x > 0) и отрицательной (x < 0). Реактивная мощность, если не считать излучения, неизменно возвращается в цепь. Легко видеть, что:
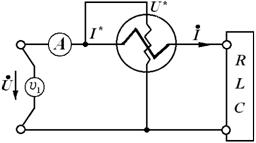
где Ia и Ip – активная и реактивная составляющие тока. Величина активной мощности на участке цепи (и в цепи, и в целом) измеряется прибором, называемым ваттметром. Этот прибор (схематично) имеет две обмотки – токовую и напряжения (рис. 2.33).
Рис. 2.33
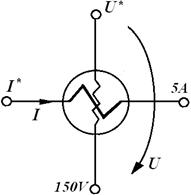
Одна из клемм токовой обмотки обозначается I* и является ее началом, вторая клемма (конец обмотки) показывает предел измерения мощности по току (например, 5А). При правильно включенном приборе выбранное в схеме направление в токе должно быть направлено от начала обмотки к ее концу. Токовая обмотка прибора выполняет функцию амперметра и включается так, чтобы через нее проходил весь ток нагрузки, в которой измеряется мощность, т.е. обмотка включается последовательно с нагрузкой (как амперметр). Как и обмотка амперметра она имеет очень малое сопротивление и теоретически никак не влияет на работу цепи. Иногда она называется последовательной обмоткой. Обмотка напряжения (параллельная обмотка) выполняет роль вольтметра и подключается к зажимам нагрузки так, чтобы фиксируемое падение напряжения, формирующее вместе с током мощность Р было направлено от клеммы U* (начало обмотки) к клемме, определяющей предельное значение напряжения (например, 150 V). Для измерения мощности в любом пассивном двухполюснике, например, в обобщенном приемнике, ваттметр должен быть включен так, как показано на рис. 2.34.
Рис. 2.34
В этом случае клеммы со звездочками объединяются и включаются на сторону источника. Если расчет цепи ведется в символической форме и Произведение Если
Это значит, что активная мощность есть вещественная (реальная) составляющая комплекса
Часть 3. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИМВОЛИЧЕСКИМ МЕТОДОМ Теоретическая электротехника располагает большим арсеналом методов расчета цепей синусоидального тока. Все эти методы детально исследованы и обоснованы во всех учебниках по теории электрических цепей. Поэтому в настоящем учебном пособии рассматривается только использование этих методов для расчета и анализа цепей всех видов и конфигураций с помощью основных наиболее часто применяемых методов. Наряду с законами Ома и Кирхгафа к таким методам относятся: - метод эквивалентных преобразований; - метод наложения; - метод контурных токов; - метод узловых потенциалов. Другие методы (пропорциональных величин, эквивалентного генератора и др.) используются только для решения некоторых специфических задач. Расчет любой электрической цепи символическим методом состоит из трех этапов: 1. Анализ цепи с целью четкого определения ее структуры, узлов, ветвей, контуров и определение неизвестных, т.е. цели расчета. 2. Перевод реальной электрической цепи (оригинала) в символическую форму путем замены реальных величин - оригиналов их комплексными изображениями, т.е. в каждой k-той ветви:
Rk → Rk, Lk → Zk = Rk + jXk = Rk + j (XLk - Xck) = Zk∟φk , где
Или при (необходимости) их проводимостей
Где 3. Выбор оптимального метода расчета. 4. Расчет цепи выбранным методом в символической форме и определение комплексных изображений искомых величин. 5. Перевод найденных комплексных изображений в область оригиналов (реальных величин). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 545. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
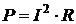 [А2×Ом = В×А = Вт].
[А2×Ом = В×А = Вт].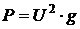 ,
,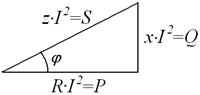
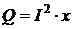 называется реактивной мощностью, учитывающей присутствие в цепи реактивного сопротивления х и степень его влияния на работу цепи.
называется реактивной мощностью, учитывающей присутствие в цепи реактивного сопротивления х и степень его влияния на работу цепи.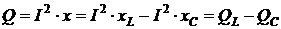 ,
,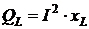 в катушке индуктивности и емкостной
в катушке индуктивности и емкостной 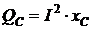 в конденсаторе реактивных мощностей. Поскольку эти мощности имеют разные знаки, в цепи они компенсируют друг друга.
в конденсаторе реактивных мощностей. Поскольку эти мощности имеют разные знаки, в цепи они компенсируют друг друга. , имеющая размерность «Вольт-Ампер», называется полной или кажущейся мощностью, формируемой величиной полного или кажущегося сопротивления z.
, имеющая размерность «Вольт-Ампер», называется полной или кажущейся мощностью, формируемой величиной полного или кажущегося сопротивления z.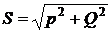 ,
, 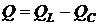 ,
,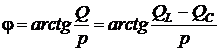 ,
,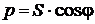 ,
, 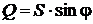 .
.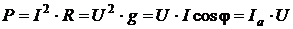 ;
;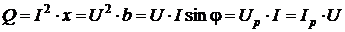 ,
,
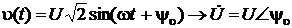 , а
, а 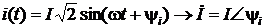 , полную информацию о мощностях на участке цепи дает комплексное число
, полную информацию о мощностях на участке цепи дает комплексное число 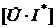 , где I* – сопряженный комплекс тока, т.е. при
, где I* – сопряженный комплекс тока, т.е. при 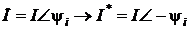 .
.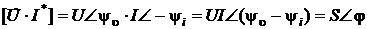 , т.е. модуль (величина) комплексного числа
, т.е. модуль (величина) комплексного числа 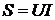 .
.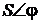 перевести в алгебраическую форму, получим:
перевести в алгебраическую форму, получим: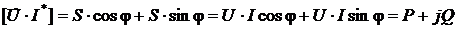 .
.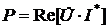 , а реактивная мощность, есть мнимая составляющая этого комплекса, т.е.
, а реактивная мощность, есть мнимая составляющая этого комплекса, т.е. 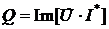 – импеданс.
– импеданс.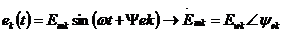
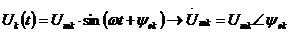 ,
,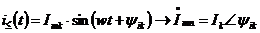 ,
,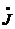 XLk, Ck →
XLk, Ck → 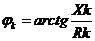
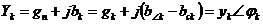 ,
,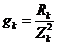 ,
, 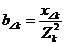 и
и 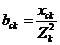 ,
, 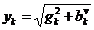 ,
,