
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные сведения о синусоидальных функциях
Основной формой записи синусоидальной функции времени является:
Применительно к электрическим цепям под a(t) можно понимать и синусоидальные ЭДС:
и электрическое напряжение:
и ток:
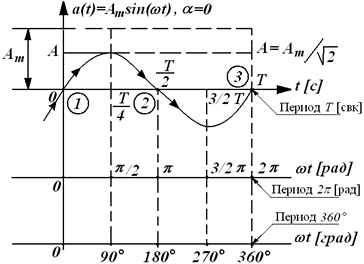
Коэффициент Аm при синусоиде (Em, Um, Im) есть наибольшее значение синусоидальной функции и называется амплитудой. Размерность амплитуды совпадает с размерностью собственно синусоидальной функции [Вольт, Ампер]. Величина Т [сек] называется периодом синусоиды, т.е. периодом повторения однозначных значений синусоидальной функции. Аргумент синуса Величина 1/Т = f [1/сек] = Гц (Герц)] называют частотой изменения синусоидальной функции, а величину 2p/Т = 2pf – угловой частотой (смысл названия «угловая» частота будет объяснен позднее). В связи с этим в электротехнике синусоидальная функция обычно записывается так: a(t) = Am×sin (wt + a). Это означает, что любая синусоида определяется тремя величинами: – амплитуда Аm(Em, Um, Im); – частота w(f); – начальная фаза Синусоида считается известной, если известны эти три величины. На рис. 2.1 представлено графическое изображение синусоиды, начальная фаза которой равна нулю.
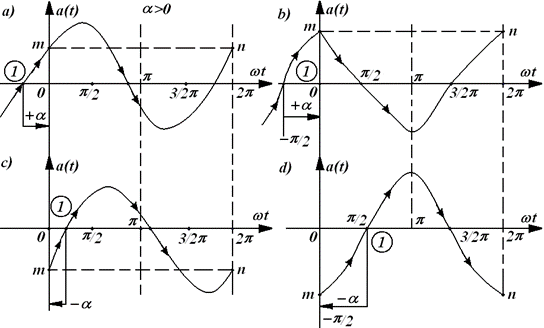
Рис. 2.1 Как показано на графике, синусоида может быть представлена и как функция времени t[сек], и как функция зависящего от времени угла wt, измеряемого или в радианах (период 2p) или в градусах (период 360°). На рис. 2.2 представлены графики синусоид с разными начальными фазами. На графике начальная фаза любой синусоиды, отсчитывается от ближайшей к началу координат точки перехода синусоиды (в положительном направлении оси абсцисс), от отрицательных значений к положительным через ноль до начала координат. При этом, если отсчет ведется в положительном направлении оси абсцисс, начальная фаза положительна, а при отсчете в отрицательном направлении – отрицательна. 
Рис. 2.2
Это означает, что начальная фаза синусоиды рис. 2.1 равна нулю (отсчет от точки 1). Начальная фаза синусоиды рис. 2.2,а, отсчитываемая от точки 1 до нуля, положительна (a > 0) и имеет произвольное значение. Начальная фаза синусоиды рис. 2.2,b положительна и равна Соответственно (отсчет от точки 1 до нуля) начальная фаза синусоиды рис. 2.2,с a < 0, а рис. 2.2,d Приведенные графики и общее выражение для фазы синусоиды Значения синусоиды а(t) в каждый момент времени tк, т.е. а(tк) называются мгновенными значениями. Наряду с мгновенными значениями и амплитудой синусоиды вводится понятии действующего значения, под которым понимается среднеквадратичное за период значение синусоиды и обозначается просто А(Е, U, I). Легко показать, что действующее значение и амплитуда связаны соотношением
Действующие значения синусоидальных величин являются основными показателями и характеристиками ЭДС, токов и напряжений, поскольку все силовые (энергетические) проявления электрического тока и напряжения определяются их действующими значениями. Все измерительные приборы основных промышленных систем (электромагнитные, электродинамические и т.п.) фиксируют именно действующие значения синусоидальных величин. Таким образом, синусоидальные ЭДС, токи и напряжения однозначно определяются амплитудой (или действующим значением), частотой и начальной фазой. Это значит, что найти, например, синусоидальный ток означает, что необходимо найти не одну (как в случае постоянного тока), а три величины: Im(I), w и yi. Это относится и к ЭДС, и к напряжению, и само по себе уже указывает на то, что расчет цепей синусоидального тока является более сложным, чем цепей постоянного тока. Более сложными оказываются, в том числе и математические действия над синусоидальными функциями (величинами). Например, известно, что результатом сложения двух (или более) синусоид является синусоида. Однако, определить эту синусоиду (ее амплитуду, частоту и начальную фазу) по известным слагаемым в рамках обычных инженерных расчетов практически невозможно, поскольку в тригонометрии приемлемые для таких расчетов формулы отсутствуют.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 507. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
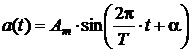 .
. ,
,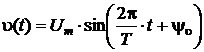 ,
,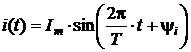 .
.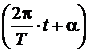 называют фазой синусоиды, а значение этой фазы в начальный момент времени (t = 0), т.е.
называют фазой синусоиды, а значение этой фазы в начальный момент времени (t = 0), т.е. 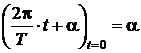 называют начальной фазой. И фаза, и начальная фаза измеряются или в радианах (при периоде синусоиды 2p) или в градусах (при периоде синусоиды 360°).
называют начальной фазой. И фаза, и начальная фаза измеряются или в радианах (при периоде синусоиды 2p) или в градусах (при периоде синусоиды 360°). .
.
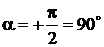 .
.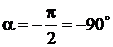 .
.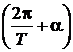 указывают на уникальное свойство синусоидальных функций, а именно: синусоиды, в координатах [а(t) ¸ t] имеют разные по времени периоды Т [сек] и, как следствие, – разные частоты f = 1/T (рис. 2.1), а в координатах [а(wt) ¸ (wt)], при разных частотах имеют один и тот же период 2p или 360°. Следует понимать при этом, что масштабные коэффициенты в радианах для синусоид разных частот будут разными. Это означает, что на одном и том же графике в координатах [а(wt) ¸ (wt)] можно строить и сравнивать только синусоиды одной и той же частоты.
указывают на уникальное свойство синусоидальных функций, а именно: синусоиды, в координатах [а(t) ¸ t] имеют разные по времени периоды Т [сек] и, как следствие, – разные частоты f = 1/T (рис. 2.1), а в координатах [а(wt) ¸ (wt)], при разных частотах имеют один и тот же период 2p или 360°. Следует понимать при этом, что масштабные коэффициенты в радианах для синусоид разных частот будут разными. Это означает, что на одном и том же графике в координатах [а(wt) ¸ (wt)] можно строить и сравнивать только синусоиды одной и той же частоты.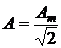 , т.е.:
, т.е.: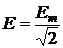 ;
; 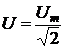 ;
; 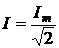 .
.