
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Комплексные числа и математические действия над ними
Конечно, комплексные числа и математические действия над ними детально изучаются в курсах математики. Однако, опыт показывает, что в связи с ограниченным их использованием в учебных курсах за пределами математики и отсутствием в связи с этим практических навыков вычислений большинство студентов при использовании комплексных чисел испытывают значительные затруднения. В то же время математический аппарат, связанный с использованием комплексных чисел, составляет основу теории расчета электрических цепей. Включение в пособие раздела комплексных чисел в связи с этим вполне оправдано.
Общие положения
Если натуральные числа располагаются на оси, комплексные числа располагаются на плоскости. Ось абсцисс координатной плоскости комплексных чисел является осью вещественных единиц (+1, –1), а ось ординат – мнимых единиц (+j, –j). В электротехнике мнимая единица обозначается буквой Комплексные числа представляют в двух формах. Например, на обычной декартовой координатной плоскости (рис. 2.3) комплексное число, соответствующее точке А комплексной плоскости, записывается
Такая форма записи комплексного числа называется алгебраической.
Рис. 2.3
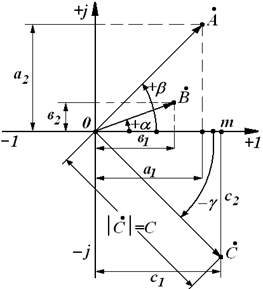
Комплексное число может быть записано и в полярных координатах. В этом случае комплексное число Здесь  Понятно, что одному и тому же комплексному числу на векторной плоскости соответствует один единственный вектор, т.е. между комплексными числами и соответствующими им векторами существует взаимно-однозначные соответствия. Это оказывается чрезвычайно полезным для построения векторных диаграмм при расчетах и анализе электрических цепей. Углы a, b и g являются аргументами комплексных чисел, измеряются в градусах или радианах. Эти углы отсчитываются от положительной полуоси вещественных (+1). При этом положительные углы отсчитываются против часовой стрелки (+a, +b), а отрицательные – по часовой (–g). Такая форма записи комплексного числа называется показательной. Правила перевода комплексных чисел из алгебраической формы записи в показательную и обратно легко увидеть из рис. 2.3. Например, для числа а1 = А×cosa; а2 = А×sina. И так для любого комплексного числа. Например, для
с1 = С×cos(–g) = С×cosa; с2 = С×sin(–g). При этом Умение переводить комплексные числа из одной формы записи в другую для расчета цепей является чрезвычайно важным. Примеры. 1. Это число записано в алгебраической форме. В показательной форме это число записывается так:
Здесь модуль (величина) комплексного числа 2. Это комплексное число находится во втором квадранте комплексной плоскости (–3, +j8), а аргумент (угол) отсчитывается от положительной полуоси вещественных. 3.
т.е. При переходе от одной формы записи комплексного числа к другой можно знать следующее: 1. Комплексное число
Рис. 2.4
В этом случае 2. Комплексное число
Рис. 2.5
В этом случае Например, если Обратный перевод этого комплексного числа в алгебраическую форму при 150° = 90° + 60° приводит к
3. Комплексное число
Рис. 2.6 В этом случае 4. Комплексное число
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 478. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
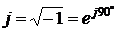 . При этом любой точке координатной плоскости соответствует одно единственное конкретное комплексное число.
. При этом любой точке координатной плоскости соответствует одно единственное конкретное комплексное число.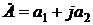 , а точке В –
, а точке В – 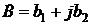 . Здесь а1 и b1 – вещественные (реальные – Real [Re]) составляющие комплексных чисел [Re], а а2 и b2 – мнимые (Impedance – Im) составляющие [Im], так что:
. Здесь а1 и b1 – вещественные (реальные – Real [Re]) составляющие комплексных чисел [Re], а а2 и b2 – мнимые (Impedance – Im) составляющие [Im], так что:

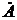 записывается как
записывается как  ,
, 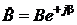 , а
, а 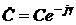 .
.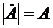 ,
, 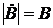 и
и 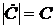 есть модули (величины) комплексных чисел и равны длине лучей, исходящих из начал координат
есть модули (величины) комплексных чисел и равны длине лучей, исходящих из начал координат  ,
, 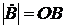 и
и 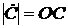 . Часто эти лучи являются векторами, представляющими соответствующие комплексные числа. Очень часто в целях упрощения записи набора текстов показательная форма комплексного числа записывается в виде
. Часто эти лучи являются векторами, представляющими соответствующие комплексные числа. Очень часто в целях упрощения записи набора текстов показательная форма комплексного числа записывается в виде  , т.е. множитель
, т.е. множитель 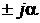 заменяется символом
заменяется символом 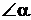 .
. , и
, и 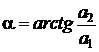 . С другой стороны, при известных А и a находим:
. С другой стороны, при известных А и a находим: имеем:
имеем: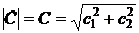 ,
,  ,
,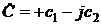 .
.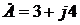 , Re[3 + j4] =3, Im[3 + j4] = 4.
, Re[3 + j4] =3, Im[3 + j4] = 4.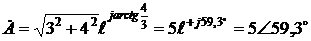 .
. , а аргумент a=59,3°.
, а аргумент a=59,3°. .
.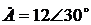 . Алгебраическая форма этого числа
. Алгебраическая форма этого числа ,
, , а
, а 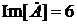 .
.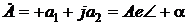 находится в первом квадранте комплексной плоскости (рис. 2.4).
находится в первом квадранте комплексной плоскости (рис. 2.4).
 ,
, 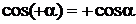 ,
, 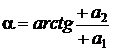 .
.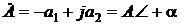 находится во втором квадранте комплексной плоскости (рис. 2.5), т.е
находится во втором квадранте комплексной плоскости (рис. 2.5), т.е  .
.
 ,
, 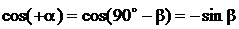 ,
, 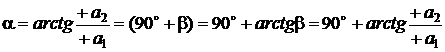 .
.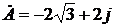 , то
, то  , а
, а 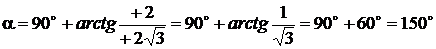 и
и 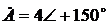 .
.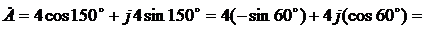
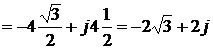 .
.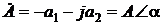 находится в третьем квадранте комплексной плоскости (рис. 2.6), т.е
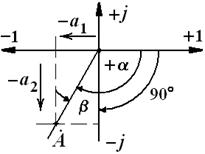
находится в третьем квадранте комплексной плоскости (рис. 2.6), т.е  .
.
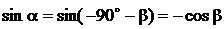 ,
, 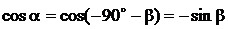 ,
,  .
.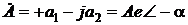 находится в четвертом квадранте комплексной плоскости. Здесь
находится в четвертом квадранте комплексной плоскости. Здесь 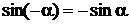 ,
,  ,
, 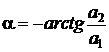 .
.