
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Реакція літака на східчасте відхилення руля висоти.Розподіл поздовжнього руху на довгоперіодичний Та короткоперіодичний При східчастому відхиленні руля висоти виникає момент Мz(dв), який обертає літак з кутовою швидкістю wz навколо поперечної осі ОZ, при цьому змінюється кут тангажа та кут атаки (рис. 2.1).
Зміна кута атаки викликає приріст піднімальної сили DYa(Da) і відповідний цьому момент поздовжньої статичної стійкості Мz(Da), який протидіє моменту Мz(dв) і на певному куті атаки його компенсує. Зміна кута атаки припиняється, але оскільки літак володіє моментом інерції Iz, то усталювання нового значення кута атаки має коливальний характер. Кутові коливання літака демпфіруються моментом власного аеродинамічного демпфірування Мz(wz).
Приріст піднімальної сили DYa(Da) починає змінювати напрям вектора швидкості ( кута нахилу траєкторії Q), що у свою чергу впливає на кут атаки. Зберігаючи балансування моментів, синхронно зі зміною кута Q продовжує змінюватись кут тангажа, при цьому кут атаки залишається постійним. Кутові рухи на цьому інтервалі часу відбуваються з великою частотою, тобто мають короткий період, ось чому їх називають короткоперіодичними.
Взаємодія сил і моментів у короткоперіодичному русі ілюструється графом, що наведений на рис. 2.2. Після закінчення короткоперіодичного руху стає помітним зміна швидкості польоту не лише за напрямком, але також за розміром, в основному, за рахунок дії сили GsinQ. Зміна швидкості DV впливає на приріст піднімальної сили і, як наслідок, на кут нахилу траєкторії, що у свою чергу знову змінює швидкість польоту. Виникають повільно згасаючі коливання вектора швидкості за розміром та напрямком. У темпі зі зміною кута нахилу траєкторії змінюється також кут тангажа, кут атаки при цьому залишається незмінним.  Ці рухи характеризуються низькою частотою, згасають повільно тому, їх прийнято називати довгоперіодичними або фугоїдними. Типовий вигляд перехідних функцій поздовжнього руху літака при східчастому моментному збуренні приведений на рис. 2.3. Відмітимо, що при розгляданні динаміки поздовжнього руху літака не враховувалась додаткова піднімальна сила DYa(dв), яка створюється рулем висоти і яка при наборі висоти спрямована на зменшення загальної піднімальної сили. Тому, особливо для важкого літака, на першому етапі набору висоти спостерігається так звана “просадка”, тобто початкове зменшення кута нахилу траєкторії з одночасним збільшенням кута тангажа. Це відбувається доки приріст піднімальної сили DYa(Da) не компенсує силу DYa(dв). При управлінні літаком довгоперіодичні коливання практично не виникають, оскільки гасяться пілотом або системою автоматичного управління. . Передаточні функції та структурні схеми математичної Передаточна функція Наприклад, Системі рівнянь, що описують короткоперіодичний рух, відповідають рішення:
де
Тоді передаточні функції, що зв'язують кут атаки та кутову швидкість тангажа з відхиленням руля висоти, можуть бути отримані з (2.12) у вигляді:
Для того щоб передаточні функції мали стандартний вигляд, прийнятий в теорії автоматичного управління, введемо позначення:
Ураховуючи ці співвідношення, отримаємо передаточні функції (2.13) у вигляді:
Використовуючи
Традиційно найважливішим параметром, що характеризує поздовжній рух літака, є нормальне перевантаження – відношення результуючої сили до сили ваги.
де У проекції на вісь ОYа швидкісної системи координат нормальне перевантаження визначається як
Друге рівняння сил - можна записати, використовуючи перевантаження nу , у вигляді:
Лінеаризуючи це рівняння, отримаємо
Для умов програмного горизонтального польоту (sinQ0 = 0)
 . .
Ураховуючи це співвідношення, отримаємо передаточну функцію з нормального перевантаження.
де За допомогою отриманих вище передаточних функцій можна побудувати структурні схеми математичних моделей, наприклад такі, що наведені на рис. 2.5, і які в подальшому можна використовувати при аналізі контурів автоматичного управління польотом. На структурній схемі показані основні збурення, що діють на літак: Для аналізу та синтезу САУ ЛА широко застосовують частотні методи, зокрема логарифмічні амплітудно-частотні характеристики (ЛАЧХ). На рис. 2.6¼2.9 показані ЛАЧХ поздовжнього руху, які відповідають передаточним функціям (2.14) ¸ (2.17). На графіках виділені асимптотичні ЛАЧХ, на віттях яких вказаний нахил у децибелах на декаду ( дб/дек). На рис. 2.6 крім асимптотичної показані реальні ЛАЧХ
Передаточній функції з нормального перевантаження (2.18) відповідає ЛАЧХ, що аналогічна передаточній функції з кута атаки, але з низькочастотною асимптотою на рівні 20lg
Характеристика  відповідає послідовному з’єднанню простої коливальної та форсуючої ланок. Наявність форсуючої ланки забезпечує позитивний зсув за фазою навіть до частоти wa (для статично стійкого літака частота wa завжди більше частоти 1/Tq ), що значно полегшує синтез якісних контурів управління кутовою швидкістю тангажа. відповідає послідовному з’єднанню простої коливальної та форсуючої ланок. Наявність форсуючої ланки забезпечує позитивний зсув за фазою навіть до частоти wa (для статично стійкого літака частота wa завжди більше частоти 1/Tq ), що значно полегшує синтез якісних контурів управління кутовою швидкістю тангажа.
Перехідні характеристики математичної моделі поздовжнього короткоперіодичного руху у відповідь на східчасте моментне збурення наведені на рис. 2.10. У подальшому отримані математичні моделі будуть використовуватись для аналізу та синтезу контурів автоматичного управління поздовжнім рухом літака. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 717. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 це відношення зображення вихідної величини Uвих(p) до зображення вхідної величини Uвх(p) при нульових початкових умовах. Особливість передаточних функцій літака як об'єкта управління це те, що відношення зображень береться з оберненим знаком. Це пов'язується з тим, що в аеродинаміці прийнято за позитивні відхилення органів управління вважати відхилення, що створюють негативні прирости кутових параметрів руху літака. Ось чому доцільно мати від'ємний знак і перед передаточною функцією.
це відношення зображення вихідної величини Uвих(p) до зображення вхідної величини Uвх(p) при нульових початкових умовах. Особливість передаточних функцій літака як об'єкта управління це те, що відношення зображень береться з оберненим знаком. Це пов'язується з тим, що в аеродинаміці прийнято за позитивні відхилення органів управління вважати відхилення, що створюють негативні прирости кутових параметрів руху літака. Ось чому доцільно мати від'ємний знак і перед передаточною функцією. .
. (2.12)
(2.12) - характеристичний поліном (головний визначник системи рівнянь 2.11) з коефіцієнтами:
- характеристичний поліном (головний визначник системи рівнянь 2.11) з коефіцієнтами: ;
;  .
. (2.13)
(2.13)
 звідки
звідки  ;
;

 .
. ; (2.14)
; (2.14) . (2.15)
. (2.15) та
та  , отримаємо передаточні функції:
, отримаємо передаточні функції: ; (2.16)
; (2.16) . (2.17)
. (2.17)
 ,
, – результуюча сила;
– результуюча сила;  - тяга двигуна,
- тяга двигуна,  - результуюча аеродинамічна сила,
- результуюча аеродинамічна сила,  - сила ваги.
- сила ваги. .
. -
- .
. .
.
 , (2.18)
, (2.18) .
.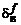 - моментні збурення (наприклад, випуск шасі), що еквівалентні відхиленню руля висоти;
- моментні збурення (наприклад, випуск шасі), що еквівалентні відхиленню руля висоти;  - збурення, що порушують баланс сил у вертикальній площині (наприклад, скидання вантажу, або зміна піднімальної сили під впливом вертикального потоку повітря).
- збурення, що порушують баланс сил у вертикальній площині (наприклад, скидання вантажу, або зміна піднімальної сили під впливом вертикального потоку повітря). для різних коефіцієнтів згасання xa
для різних коефіцієнтів згасання xa . При керуванні кутом атаки ( перевантаженням ) математична модель поздовжнього руху є проста коливальна ланка з xa < 1.
. При керуванні кутом атаки ( перевантаженням ) математична модель поздовжнього руху є проста коливальна ланка з xa < 1.
 Передаточній функції з кута тангажа відповідає характеристика
Передаточній функції з кута тангажа відповідає характеристика  , яку можна отримати якщо скласти частотну характеристику
, яку можна отримати якщо скласти частотну характеристику