
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференцируемость функции в точке.ОпределениеФункция y=f(x) называется дифференцируемойв точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0. Дифференцируемость и непрерывность (с доказательством). Теорема Доказательство Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A. Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A . Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy.
Связь дифференцируемости с непрерывностью функции в точке. Теорема Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке. Доказательство Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции. Обратное утверждение не верно.  Например, функция y=∣x∣ непрерывна в точкеx=0, но не дифференцируема в этой точке. Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.
Правила дифференцирования. Производная сложной функции. Производная линейной функции. Производная суммы, произведения, частного. Производная логарифма. Правила вычисления производных Пусть функции 1. Константу можно выносить за знак производной.
2. Производная суммы/разности. Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
Пример
3. Производная произведения.
4. Производная частного.
Производная сложной функции равна производной этой функции по промежуточному аргументу
Теорема (О производной обратной функции) Если функция Производная линейной функции Формула
Производная линейной функции равна константе, стоящей возле переменной Следствие Согласно правилам дифференцирования, константу можно выносить за знак производной, то есть
По таблице производных производная независимой переменной
В более общем случае, когда имеем выражение
В первом слагаемом выносим константу за знак производной, и производная от константы равна нулю:
Итак, окончательно имеем, что
Производная логарифма Формула
Производная логарифмической функции по основанию Напомним, что есть специальные обозначения для логарифмов: · Десятичный логарифм, · Натуральный логарифм, |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  имеют производные в точке
имеют производные в точке  . Тогда
. Тогда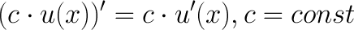


 5. Производная сложной функции.
5. Производная сложной функции. , умноженной на производную от промежуточного аргумента
, умноженной на производную от промежуточного аргумента  и
и 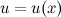 имеют производные соответственно в точках
имеют производные соответственно в точках  и
и  . Тогда
. Тогда
 непрерывна и строго монотонна в некоторой окрестности точки
непрерывна и строго монотонна в некоторой окрестности точки  имеет производную в точке
имеет производную в точке  , причем
, причем 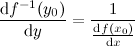 .
.
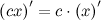

 , вместо просто
, вместо просто 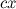 , поступаем следующим образом. Как известно, согласно свойствам производной, производная от суммы равна сумме производных, поэтому
, поступаем следующим образом. Как известно, согласно свойствам производной, производная от суммы равна сумме производных, поэтому


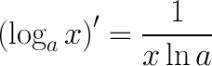
 равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.
равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания. - это логарифм по основанию 10, то есть
- это логарифм по основанию 10, то есть  ;
; - это логарифм по основанию
- это логарифм по основанию  , то есть
, то есть 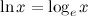 .
.