
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Второй замечательный предел1 Второй замечательный предел:
Следствия из второго замечательного предела 1° 2° 3° 4° 5° 6° Непрерывность функции. Точка разрыва первого и второго рода. Точки разрыва функции и их классификация Определение точки разрыва Определение Точка 1. функция 2. существует конечный предел функции 3. это предел равен значению функции в точке называется точкой разрыва функции. Пример Функция Точка разрыва первого рода Определение Если в точке Пример
Точка разрыва второго рода Определение Если хотя б один из пределов Пример Для функции
Точка устранимого разрыва Определение Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции Пусть заданы две функции Пусть функция  Теорема Пусть функция Теорема Если функция
Понятие производной. Геометрический и механический смысл. Понятие производной Пусть задана некоторая функция Приращение аргумента и функции Определение Приращением аргумента называется разность между двумя значениями аргумента: "новым" и "старым". Обычно обозначается как Приращением функции
Определение производной Определение Производной
или
Дифференцируемость и непрерывность. Дифференцирование функции Определение Операция нахождения производной функции называется дифференцированием этой функции. Функция Функция Теорема (О непрерывности функции в точке) Если функция Замечание. Обратное заключение не всегда верно: если функция Определение Функция
где Теорема (О необходимом и достаточном условии дифференцируемости) Для того чтобы функция Теорема устанавливает, что для функции Теорема. Если функция Доказательство. По определению производной
Это предельное равенство означает, что выражение под знаком предела можно представить в виде
где α(x) – бесконечно малая функция при x → a. Тогда
Следовательно, Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке.
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 270. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |







 , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: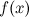 определена в точке и ее окрестности;
определена в точке и ее окрестности;
 не определена в точке
не определена в точке  , а значит, эта точка является точкой разрыва указанной функции.
, а значит, эта точка является точкой разрыва указанной функции. и
и  , такие, что
, такие, что  , то точка
, то точка  точка
точка  - точка разрыва второго рода, так как
- точка разрыва второго рода, так как  .
. или функция
или функция 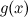 , непрерывные на некотором множестве
, непрерывные на некотором множестве  . Сумма, произведение и частное (при условии, что
. Сумма, произведение и частное (при условии, что  ) является также непрерывной функцией на рассматриваемом множестве.
) является также непрерывной функцией на рассматриваемом множестве. задана на множестве
задана на множестве  - множество значений этой функции. Пусть на множестве
- множество значений этой функции. Пусть на множестве  , которая называется композицией функций (или сложной функцией)
, которая называется композицией функций (или сложной функцией)  .
.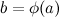 . Тогда композиция этих функций
. Тогда композиция этих функций  , которые лежит на оси абсцисс, то и обратная функция
, которые лежит на оси абсцисс, то и обратная функция  также непрерывна и монотонна на некотором отрезке
также непрерывна и монотонна на некотором отрезке  оси ординат. Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
оси ординат. Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке. . Возьмем какое-нибудь значение
. Возьмем какое-нибудь значение  из области определения этой функции:
из области определения этой функции:  . Соответствующее значение функции в этой точке будет равно
. Соответствующее значение функции в этой точке будет равно  .
. .
. , называется величина:
, называется величина:
 от функции
от функции  к приращению аргумента
к приращению аргумента  :
:  при
при  , если он существует, то есть:
, если он существует, то есть:

 или называется дифференцируемой в этом интервале, если производная
или называется дифференцируемой в этом интервале, если производная  существует в каждой точке этого интервала.
существует в каждой точке этого интервала. бесконечную производную, если в этой точке
бесконечную производную, если в этой точке  .
.
 - число, не зависящее от
- число, не зависящее от  - б.м. функция при
- б.м. функция при  дифференцируема в некоторой точке a, то она непрерывна в этой точке.
дифференцируема в некоторой точке a, то она непрерывна в этой точке.

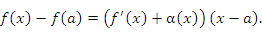
 при x → a.
при x → a.