Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правила дифференцирования. Производная обратной функции. Производная степенной и показательной функции. Логарифмическое дифференцирование.Производная обратной функции Формула
Известно свойство степеней, что
тогда
Используя производную степенной функции:
будем иметь:
Производная степенно-показательной функции Определение Степенно-показательной функцией (или показательно-степенной, или функцией в степени функция) называется функция вида Рассмотрим способы нахождения ее производной. Ый способ Применяя формулу:
То есть вначале производная берется как от степенной функции, а потом как от показательной. Замечание Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:
Задание. Найти производную функции Решение. Применяем формулу. В рассматриваемом случае
Тогда имеем:
Ответ.
Ой способ С помощью логарифмического дифференцирования:
Пример задание. Найти производную функции Решение. Прологарифмируем левую и правую часть заданной функции, будем иметь:
По свойствам логарифмов в правой части полученного равенства степень подлогарифмической функции выносим перед логарифмом:
Дифференцируем левую и правую часть равенства. Слева берем производную как от сложной функции(так как
А тогда
Ответ.
Ий способ Представим функцию
Тогда
Пример Задание. Найти производную функции Решение. Представляем функцию в следующем виде: 
Далее находим производную, от экспоненты берем производную как от сложной функции (см.производные сложных функций):
Ответ.
Логарифмическое дифференцирование Для функций вида Суть метода логарифмического дифференцирования Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция
Далее продифференцируем полученное равенство при условии, что
А тогда, выражая искомую производную
Пример Задание. Найти производную функции Решение. Если находить производную данной функции, используя таблицу производных и правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического дифференцирования. Прологарифмируем левую и правую части заданной функции:
Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:
Таким образом, получаем, что логарифм заданной функции равен:
Дифференцируем левую и правую часть последнего равенства, не забывая, что
Итак,
Отсюда
Подставляя вместо функции
Ответ. |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 249. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
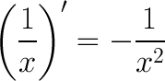





















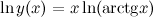
 - это функция от переменной
- это функция от переменной  ), а справа - как производную произведения:
), а справа - как производную произведения: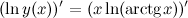



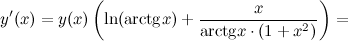
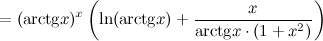



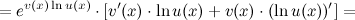


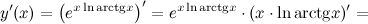




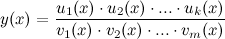 для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.
для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование. . Прологарифмируем левую и правую части данного выражения:
. Прологарифмируем левую и правую части данного выражения:

 , в результате имеем:
, в результате имеем: