Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Найпростіші властивості векторного простору.Властивість 1. У довільному векторному просторі існує лише один нульовий вектор. Доведення. Припустимо, що знайшовся такий векторний простір V, у якому декілька різних нульових елементів: Розглянемо суму За означенням нульового вектора За означенням нульового вектора Згідно із припущенням, Властивість доведено. Властивість 2. У довільному векторному просторі для кожного вектора існує лише єдиний протилежний. Доведення. Припустимо, що у деякому векторному просторі V знайшовся вектор Розглянемо суму За означенням протилежного вектора За означенням протилежного вектора Згідно із припущенням, Властивість доведено. Надалі для зручності позначатимемо операції додавання і множення у векторному просторі як "+" і " Теорія визначників n-го порядку.
Для введення поняття визначника Перестановки з n символів. Означення 1. Перестановкою з Означення 2. Транспозицією називається таке перетворення перестановки, при якому два її елементи міняються місцями. Теорема 1. З Доведення.  Застосуємо метод математичної індукції по кількості символів n. 1. При 2. Зробимо індуктивне припущення: з 3. Покажемо справедливість індуктивного переходу для Розглянемо всі перестановки з
Ця група знаходиться в умовах індуктивного припущення. За індуктивним припущенням з Запишемо всі перестановки, що починаються з двійки, трійки, тощо.
Останньою буде група перестановок, що починаються з
Таким чином всі перестановки розбиваються на k+1 клас, в кожний з яких входить k перестановок. Отже всього буде k!(k+1)=1ˑ2ˑ…ˑkˑ(k+1)=(k+1)! перестановок. З доведеного за принципом математичної індукції дане твердження є правильним при довільному натуральному Теорема 2.Усі Доведення Застосуємо метод математичної індукції по кількості символів n. При 2,1. Зробимо індуктивне припущення: вважатимемо правильним дане твердження при 1, 2, 3, ... , 1, ... Розглянувши останні На стикуванні отриманих груп перестановок першу перестановку наступної групи отримаємо з останньої за рахунок транспозиції символів, що є першими у цих групах. Теорему доведено. Означення 3. Два символи Означення 4. Перестановка називається парною, якщо загальна кількість інверсій в ній парна, і непарною в протилежному випадку. Теорема 3. Кожна транспозиція змінює парність перестановки. Доведення. При доведенні слід розглянути 2 випадки. 1. Елементи
Зауважимо, що після транспозиції положення Отже парність перестановки змінюється. 2. Між елементами
Зробимо транспозицію поступово. Будемо міняти місцями
Щоб поставити Теорему доведено. Теорема 4. При n≥2 кількість парних перестановок дорівнює кількості непарних перестановок, тобто Доведення. Запишемо всі При n≥2 Теорему доведено. Підстановки n-го степеня. Означення. Підстановкою Будемо записувати підстановку у два рядки: у першому будуть вихідні Наприклад:
Поставимо 2 питання: 1) Скільки форм запису однієї ї тієї підстановки. 2) Скільки різних підстановок n-го степеня можна скласти. На обидва питання відповідь: Розглянемо перше питання. Різні форми запису можна отримати за рахунок різного розташування стовпчиків перестановок. З теорії перестановок відомо, що їх буде n!. Розглянемо друге питання. Зафіксуємо елементи у першому рядку. Очевидно, що підстановки будуть різними, якщо відрізняються відповідно образи у другому рядку. Отже кількість підстановок дорівнюватиме кількості перестановок елементів другого рядка, а їх, як відомо, n!. Означення. Підстановка називається парною, якщо парності верхньої і нижньої перестановок однакові, тобто обидві перестановки або парні або непарні. Означення. Підстановка називається парною, якщо загальна кількість інверсій верхньої і нижньої перестановок є парним числом, в супротивному разі перестановка непарна. Теорема. При n≥2 кількість парних підстановок дорівнює кількості непарних підстановок, тобто дорівнює Запишемо всі підстановки у вигляді:
Твердження теореми випливає з відповідної теореми для перестановок. Дійсно, тоді парність підстановки визначається лише парністю нижньої перестановки, а парних нижніх існує Зауваження. Для самостійного доведення залишається факт, що означення парності підстановки не залежить від форми запису цієї підстановки. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 340. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 і
і  .
. .
. .
.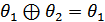 .
.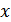 , для якого є декілька різних протилежних елементів:
, для якого є декілька різних протилежних елементів:  та
та 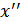 .
. . Скористуємось також асоціативністю додавання.
. Скористуємось також асоціативністю додавання.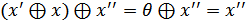
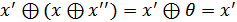
 ", маючи на увазі абстрактні операції "
", маючи на увазі абстрактні операції "  " і "
" і "  ".
".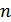 -го порядку потрібна інформація з теорії перестановок і підстановок.
-го порядку потрібна інформація з теорії перестановок і підстановок.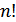 перестановок.
перестановок.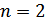 це твердження є правильним, бо маємо дві перестановки: 1 2, 2 1.
це твердження є правильним, бо маємо дві перестановки: 1 2, 2 1. символів можна скласти
символів можна скласти  перестановок.
перестановок.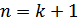 .
.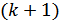 символів за такою схемою. Запишемо спочатку всі перестановки, що починаються з одних одиниць.
символів за такою схемою. Запишемо спочатку всі перестановки, що починаються з одних одиниць.

 .
.
 . Доведемо справедливість твердження при
. Доведемо справедливість твердження при 
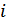 та
та  , але в перестановці знаходиться раніше.
, але в перестановці знаходиться раніше.
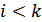 , то загальна кількість інверсій навпаки збільшиться на одну.
, то загальна кількість інверсій навпаки збільшиться на одну.
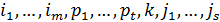
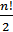 .
. – парне число, тому список має парну кількість перестановок, половина з яких є парними, половина – непарними.
– парне число, тому список має парну кількість перестановок, половина з яких є парними, половина – непарними.