
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
IV. Подвійний векторний добуток.1. Поняття подвійного векторного добутку. Означення. Подвійним векторним добутком трьох векторів Алгебраїчні властивості подвійного векторного добутку є наслідками алгебраїчних властивостей векторного добутку. Існує зв’язок між подвійним векторним добутком і лінійними операціями над векторами. Цей зв’язок здійснюється за формулою
Доведення. (Довести цю формулу) Поняття лінійного простору. Означення 1. Говоритимемо, що у множині М визначена внутрішня бінарна алгебраїчна операція, якщо будь-якій упорядкованій парі елементів Означення 2. Говоритимемо, що в множині M визначена зовнішня операція над множиною P, якщо будь-якій парі елементів Операція додавання векторів (геометричних) відноситься до внутрішніх операцій і операція множення геометричного вектора на число є прикладом зовнішньої операції, визначеної в множині геометричних векторів над множиною дійсних чисел. Означення 3. Векторним або лінійним простором називається непорожня множина V, в якій визначено дві операції над множиною дійсних чисел: внутрішня, що умовно називається додаванням, і зовнішня, що умовно називається множенням на дійсне число, і виконується 8 умов: 1. 2. 3. 4. 5.  6. 7. 8. Означення 4. Елементи множини V, що є векторним простором, називаються векторами. Приклад 1. Всі геометричні вектори простору (площини) утворюють векторний простір відносно традиційних операцій додавання геометричних векторів і множення вектора на число. Дійсно, виконання всіх вимог означення 3було обґрунтовано у векторній алгебрі. Приклад 2. (арифметичний простір) За множину V візьмемо множину всіх упорядкованих
Числа Cумою векторів Добутком вектора Можна показати за означенням, що арифметичний простір є лінійним простором. Контрприклад.За множину V візьмемо ту ж саму множину, що у прикладі 2. Операцію додавання введемо за тим же правилом. Операцію множення на число введемо іншим чином, а саме: добутком вектора В цій множині не виконується лише вимога 7.
Бачимо, Приклад 3. Розглянемо множину многочленів степеня не вищого за Операції додавання многочленів та множення на число вводиться традиційним способом. Легко перевірити виконання всіх вимог означення, тому дана множина є векторним простором відносно введених операцій. Контрприклад.Розглянемо множину многочленів лише У цьому випадку множина не є векторним простором, тому що в цій множині не визначена операція додавання. Дійсно, наведемо два многочленів, сума яких не є многочленом Наприклад, сума Приклад 4. Розглянемо множину всіх функцій, що визначені на проміжку Приклад 5. Розглянемо множину всіх функцій, що є неперервними на проміжку
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 називається векторний добуток двох векторів вектора
називається векторний добуток двох векторів вектора 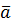 і вектора
і вектора  :
:  .
.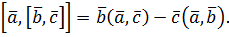
 за деяким правилом ставиться у відповідність однозначно визначений елемент zϵM.
за деяким правилом ставиться у відповідність однозначно визначений елемент zϵM.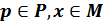 ставиться у відповідність однозначно визначений елемент множини М.
ставиться у відповідність однозначно визначений елемент множини М.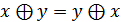 – комутативність додавання.
– комутативність додавання.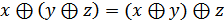 – асоціативність додавання.
– асоціативність додавання.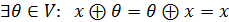 (
( 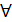 x).
x). – для довільного елемента існує протилежний до нього.
– для довільного елемента існує протилежний до нього.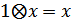 – серед множини дійсних чисел є таке, що не змінює у добутку вектор.
– серед множини дійсних чисел є таке, що не змінює у добутку вектор.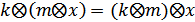
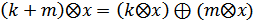

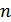 чисел.
чисел.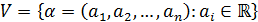
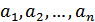 назвемо компонентами вектора.
назвемо компонентами вектора.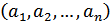 і
і  назвемо вектор, утворений сумою відповідних компонент:
назвемо вектор, утворений сумою відповідних компонент:  .
. назвемо вектор
назвемо вектор 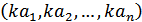 .
. .
.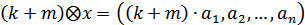
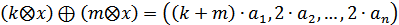
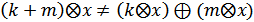 , отже ця множина не є лінійним простором.
, отже ця множина не є лінійним простором.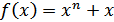 та
та  є многочленом 1-го степеня.
є многочленом 1-го степеня.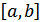 . Додавання і множення функцій на число введемо традиційним способом, як у математичному аналізі. При цьому також виконуються всі вимоги означення векторного простору, тому дана множина відносно введених операцій є векторним простором.
. Додавання і множення функцій на число введемо традиційним способом, як у математичному аналізі. При цьому також виконуються всі вимоги означення векторного простору, тому дана множина відносно введених операцій є векторним простором.