
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрична інтерпретація поняття лінійної залежності.З’ясуємо геометричний зміст поняття лінійної залежності. Теорема 1. Для того, щоб система з одного вектора була лінійно залежною, необхідно і достатньо, щоб цей вектор був нульовим. Теорему 1 було обґрунтовано у зауваженні попереднього параграфу. Теорема 2. Необхідною і достатньою умовою лінійної залежності двох векторів є їх колінеарність. Доведення. Необхідність. Припустимо, що вектори Доведемо, що вектори колінеарні. Отже один з векторів є лінійною комбінацією. Нехай це Достатність. Припустимо, що Можливі випадки: 1) Принаймні один з векторів нульовий. Тоді твердження очевидне, тому що в системі міститься лінійно залежна підсистема. 2) Обидва вектори ненульові. Для доведення потрібна така лема. Лема. Якщо Дійсно, якщо Згідно із лемою маємо, що Теорему доведено. Теорема 3. Необхідною і достатньою умовою лінійної залежності трьох векторів є їх компланарність. Доведення. Необхідність. Припустимо, що вектори Якщо серед векторів системи пара колінеарних, то очевидно, що вони є компланарними. Нехай тоді вектори попарно неколінеарні. Тоді за означенням 1 лінійної залежності існує вектор (наприклад, Візьмемо точку А і прикладемо до неї вектори

(для визначеності
Тоді з попередньої рівності випливає, що Достатність. Припустимо, що Якщо серед векторів системи пара колінеарних, то в системі є лінійно залежна підсистема і тому вся система залежна. Нехай тоді вектори попарно неколінеарні. Прикладемо вектори Оскільки Теорему доведено. Теорема 4. Довільні чотири вектори геометричного простору лінійно залежні. Доведення. Нехай маємо систему Візьмемо точку А і прикладемо до неї дані вектори. Побудуємо паралеліпіпед, діагональ якого є
За означенням додавання векторів маємо Тоді Теорему доведено. Зауваження. Мимохідь ми довели таке важливе твердження: будь-який вектор у просторі можна розкласти за трійкою некомпланарних векторів. |
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 313. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 утворюють лінійно залежну систему.
утворюють лінійно залежну систему. (для визначеності). Тоді
(для визначеності). Тоді  , тобто вектори колінеарні.
, тобто вектори колінеарні. . Покажемо, що система лінійно залежна.
. Покажемо, що система лінійно залежна. , то
, то  :
:  , то
, то  , якщо
, якщо  , то
, то  .
. утворюють лінійно залежну систему. Покажемо, що вони компланарні.
утворюють лінійно залежну систему. Покажемо, що вони компланарні. ), що є лінійною комбінацією інших
), що є лінійною комбінацією інших  .
. .
.

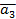
 )
)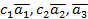 – сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки
– сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки 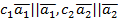 , то вектори
, то вектори 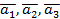 також компланарні.
також компланарні. . Тоді
. Тоді 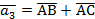 .
. , то
, то  . Тоді
. Тоді 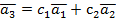 , тобто
, тобто 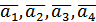 . Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає.
. Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає. , а ребра знаходяться на прямих, що містять вектори
, а ребра знаходяться на прямих, що містять вектори 
 . Оскільки
. Оскільки  , маємо
, маємо  .
. , а тому
, а тому