
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Доведення. (навести доведення)З означення скалярного добутку і отриманої формули випливає: 1) 2) II. Векторний добуток 1. Поняття векторного добутку Введемо спочатку поняття 1)правої та 2)лівої трійки векторів. Означення 1. Упорядкована трійка векторів a, b, c називається правою, якщо з кінця останнього вектора поворот від першого до другого спостерігається проти годинникової стрілки, якщо ж за годинниковою, то трійка векторів називається лівою. Тепер можна ввести поняття векторного добутку. Означення 2. Векторним добутком векторів 1) 2) вектор 3) трійка векторів
2. Геометричні та алгебраїчні властивості векторного добутку. Геометричні властивості пов’язані з векторним добутком містять дві наступні теореми. Теорема 1. (про геометричний зміст довжини векторного добутку). Довжина векторного добутку дорівнює добутку довжин цих векторів на синус кута між ними. Доведення. (навести доведення). Теорема 2. Для того щоб два вектори були колінеарними необхідно і достатньо, щоб їх векторний добуток дорівнював нульовому вектору. Доведення. (навести доведення). Розглянемо алгебраїчні властивості векторного добутку: 1) 2) 3) 4) Доведення. (навести доведення). Рекомендації щодо доведення дистрибутивності векторного добутку. Крім доведення, поданого в основному підручнику [1] (література, навчально-методична), можна запропонувати більш геометричне доведення [9]. Наведемо його.  Отже треба довести, що Ця рівність очевидна, коли принаймні один з векторів нульовий. Нехай тепер усі вектори ненульові. Проведемо спочатку доведення, в окремому випадку, коли
 . .
Спроектуємо точку А на площину, отримаємо вектор
Доведемо, що ці вектори однаково напрямлені. Вектор Перейдемо до доведення рівності Прикладемо до точки О вектори
За означенням додавання векторів маємо
Доведемо дистрибутивність в загальному випадку. Для цього подамо
що і треба було довести.
3. Вираз координат векторного добутку через координати векторів. Нехай вектори Треба знайти координати вектора Для того щоб це зробити, треба попередньо скласти таблицю множення
Доведення таблиці множення (навести доведення). Використовуючи таблицю множення, доведемо, що розкладання вектора
Доведення (навести доведення).
III. Мішаний добуток. 1. Поняття мішаного добутку Означення 1. Мішаним добутком трьох векторів
2. Геометричні та алгебраїчні властивості. Теорема 1 (про геометричний зміст мішаного добутку). Мішаний добуток векторів
Доведення (навести доведення). З цієї теореми можна отримати наслідок. Наслідок. Для того щоб три вектори Наслідком теореми 1 є також така алгебраїчна властивість
(Навести доведення цієї властивості). Оскільки з доведеної рівності виходить, що квадратні дужки можна поставити будь-як, то домовились позначати мішаний добуток так Що стосується інших алгебраїчних властивостей, то є наслідками скалярного і векторного добутку. Наприклад, можна довести, що (Навести доведення)
3. Вираз мішаного добутку через координати векторів. Нехай в ортонормованому базисі
Треба знайти вираз Користуючись властивостями скалярного і мішаного добутків, можна довести таку формулу:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


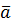 і
і 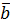 називається вектор, що умовно позначається через
називається вектор, що умовно позначається через  і задовольняє умови:
і задовольняє умови: (
( 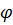 – кут між векторами
– кут між векторами  є правою.
є правою. (антикомутативність);
(антикомутативність); ;
; (дистрибутивність);
(дистрибутивність);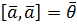 .
.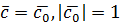 . Для цього опишемо геометричну побудову вектора
. Для цього опишемо геометричну побудову вектора  . До довільної точки O простору прикладемо вектори
. До довільної точки O простору прикладемо вектори  . Через точку O проведемо площину перпендикулярну
. Через точку O проведемо площину перпендикулярну  :
: 

 . Повернемо
. Повернемо  , отримаємо вектор
, отримаємо вектор  . Доведемо, що вектор
. Доведемо, що вектор  . Насправді ці вектори мають однакову довжину, тому що
. Насправді ці вектори мають однакову довжину, тому що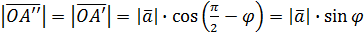 ,
,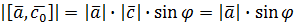 .
. .
. ,
, 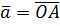 . За правилом трикутника побудуємо вектор
. За правилом трикутника побудуємо вектор  . Спроектувавши точки А і В, отримаємо вектори
. Спроектувавши точки А і В, отримаємо вектори  . Повернемо їх в площині на кут
. Повернемо їх в площині на кут  .
. . Але з наведеної вище конструкції випливає, що
. Але з наведеної вище конструкції випливає, що 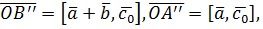
 . А тому з попередньої рівності випливає:
. А тому з попередньої рівності випливає: , де
, де  . Тоді можна записати
. Тоді можна записати ,
,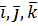 мають розкладання
мають розкладання  .
.

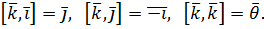

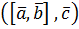 .
.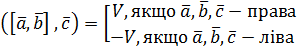
 були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
 .
.
 .
.