
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Поняття вектора, лінійні операції над векторами.
Розглянемо в просторі (на площині) множину всіх направлених відрізків. В цій множині можна по-різному ввести означення рівності напрямленнях відрізків і отримати три поняття вектора. Означення 1. Два напрямлених відрізки називаються рівними, якщо: 1) вони колінеарні (знаходяться на одній або паралельних прямих); 2) мають однаковий напрямок; 3) мають однакові довжини. Означення 2. Вільним вектором називається множина всіх рівних між собою в сенсі означення 1 напрямлених відрізків. Введемо іншим чином означення рівності. Означення 1'. Два напрямлених відрізки називаються рівними, якщо: 1) вони колінеарні; 2) мають однаковий напрямок; 3) знаходяться на одній прямій; 4) мають однакові довжини. Означення 2'. Ковзним вектором називається множина всіх рівних між собою у сенсі означення 1' напрямлених відрізків. Означення 1''. Два напрямлених відрізки називаються рівними, якщо : 1) в них рівні довжини; 2) знаходяться на одній прямій; 3) однаково направлені і мають спільний початок. Означення 2''. Зв'язаним вектором називається множина рівних між собою в сенсі означення 1'' напрямлених відрізків. З останнього означення випливає, що зв'язаний вектор дорівнює лише собі. В даному курсі розглядатимемо лише вільні вектори. Над векторами вводяться дві основні лінійні операції : 1) додавання векторів; 2) множення вектора на число. Означення 3. Сумою двох векторів  Означення 4. Добутком вектора а на число к називається вектор, що умовно позначається 1) 2) 3)
Властивості лінійних операцій (довести самостійно).
1. 2. 3. Існує так званий нульовий вектор
Зрозуміло, що початок і кінець нульового вектора збігаються, тобто він має нульову довжину, а напрямок цього вектора невизначений. 4. Для будь-якого вектора Вектори 5. 6. 7. 8. Поняття лінійно залежних і лінійно незалежних систем векторів. Означення. Лінійною комбінацією векторів Означення 1. Система векторів Інакше кажучи, Означення 2. Система векторів
Теорема. При Доведення. Нехай система векторів лінійно залежна за означенням 1.Треба довести, що вона лінійно залежна у сенсі означення 2. Скористаємось означенням 1. Тоді виконується (1):
Додамо до обох частин даної рівності вектор протилежний до
Внаслідок комутативності і означення нульового вектора маємо:
Тобто
Нехай тепер система векторів лінійно залежна за означенням 2: Треба довести, що Додамо вектор
Відомо, що
Тобто система є лінійно залежною за означенням 1. Теорему доведено. Зауваження. При Теорема. Якщо у системі векторів є лінійно залежна підсистема, то і вся система лінійно залежна. Доведення. Нехай задана система Запишемо рівність в такому виді:
Тоді Система лінійно залежна за означенням 2. Теорему доведено. Означення. Система векторів З вище доведеної теореми випливає, що якщо система лінійно незалежна, то всі її підсистеми також лінійно незалежні. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 319. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
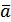 і
і 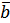 , називається вектор, що умовно позначається
, називається вектор, що умовно позначається 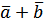 , початок якого знаходиться в початку вектора
, початок якого знаходиться в початку вектора 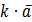 і має такі властивості:
і має такі властивості: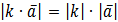
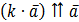 , якщо
, якщо  , і
, і 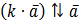 , якщо
, якщо 
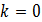 .
.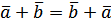 – комутативність додавання.
– комутативність додавання.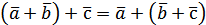 – асоціативність додавання.
– асоціативність додавання.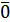 , тобто такий, для якого
, тобто такий, для якого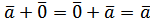 для довільного вектора
для довільного вектора 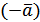 , тобто такий, що ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, тобто такий, що ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 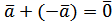 .
.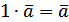 для довільного вектора
для довільного вектора 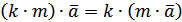 – асоціативність множення на число.
– асоціативність множення на число.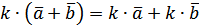 – дистрибутивність.
– дистрибутивність.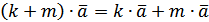 – дистрибутивність.
– дистрибутивність.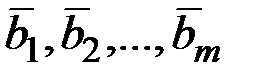 називається вектор
називається вектор 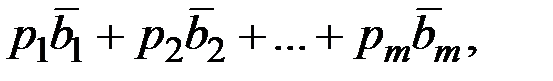 де pi- будь-які числа.
де pi- будь-які числа.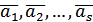 називається лінійно залежною, якщо принаймні один з векторів цієї системи є лінійною комбінацією інших.
називається лінійно залежною, якщо принаймні один з векторів цієї системи є лінійною комбінацією інших.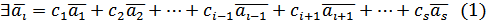 .
.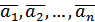 називається лінійно залежною, якщо існують числа
називається лінійно залежною, якщо існують числа 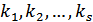 , серед яких принаймні одне
, серед яких принаймні одне 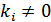 , що виконується рівність:
, що виконується рівність: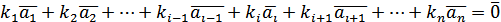
 .
.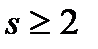 перше і друге означення лінійно залежної системи еквівалентні.
перше і друге означення лінійно залежної системи еквівалентні.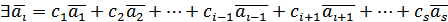 .
.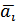 :
: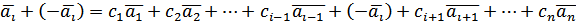
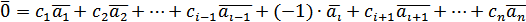
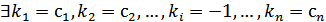 , що виконується і рівність
, що виконується і рівність 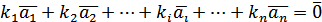 (
( 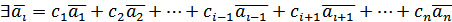 .
.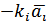 до лівої та правої частини даної рівності:
до лівої та правої частини даної рівності: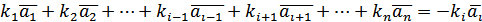
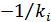 маємо:
маємо: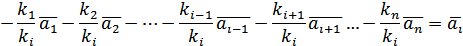
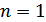 , означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність
, означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність 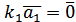 , тобто
, тобто 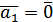 . Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий.
. Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий.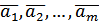 – лінійно залежна. Тоді
– лінійно залежна. Тоді 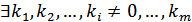 :
: 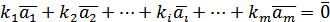 .
.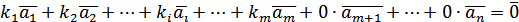
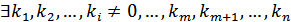 такі, що
такі, що 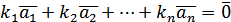 .
.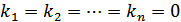 .
.