Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Визначимо щільність зв’язку між коефіцієнтом використання пробігу і продуктивністю праці.
Перевіримо істотність зв’язку: К1=6-1=5, К2=24-6=18 Fф=0,22/(1-0,22)*18/5=1.01 Fкр=2,38 В даному випадку Fкр > Fф, отже зв'язок між коефіцієнтом використання пробігу і продуктивністю праці, і вважається, що він спричинений випадковими факторами.
Іншим методом визначення взаємозв’язків між факторною і результативною ознакою метод регресії і кореляції. На першому етапі при застосуванні цього методу визначають рівняння регресії. Задача регресійно-кореляційного методу полягає у виявленні зв’язку між факторною та результативною ознаками, та виборі рівняння регресії методом найменших квадратів. Це означає, що сума різниць квадратів теоретичних і емпіричних значень повинна бути мінімальною. S(Уі - У)2® min На наступному етапі необхідно знайти параметри рівняння: У = а + b*х де а – параметр, що показує значення результативної ознаки (у), якщо факторна ознака х = 0; b – параметр, що показує на скільки одиниці змінюється у середньому результативна ознака (у), якщо факторну ознаку змінити на одиницю.
n*a + b*S x = S y a*S x + b*S x2 = S x*y Для розв’язку системи рівнянь побудуємо допоміжну таблицю. На наступному етапі проводиться оцінка щільності зв’язку. Щоб виявити щільність зв’язку, вимірюють лінійний коефіцієнт кореляції Пірсона:
Лінійний коефіцієнт кореляції r змінюється в межах - 1 < r < +1. Він показує напрямок і тісноту зв’язку між ознаками. На заключному етапі перевіряється істотність зв’язку. Fф  де Κ1 = c– 1 К2 = n – c, с—кількість коефіцієнтів в рівнянні регресії.
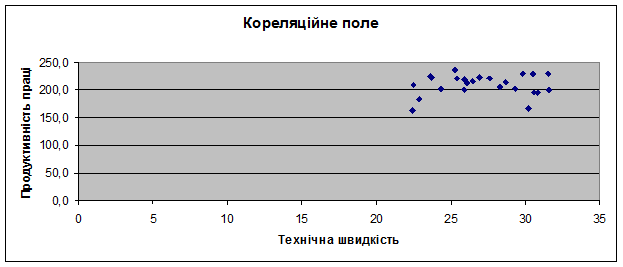
Розглянемо взаємозв’язок між технічною швидкістю (факторна ознака) і продуктивністю праці (результативна ознака). Побудуємо кореляційне поле.
Рис. 11.Кореляційне поле. Припускаємо, залежність лінійна. Побудуємо допоміжну таблицю.
Таблиця 3.8. Зв'язок між технічною швидкістю (факторна ознака) і продуктивністю праці (результативна ознака).
24а+650,3 b=5025, 650,3a+17826,5b=136254,5. а=196,375 b=0,48 Функція має вигляд: Y=196,375+0,48х. Відповідно до функції розрахуємо теоретичні значення результативної ознаки. Ці значення наведено в останньому стовпці табл. 3.13. За допомогою коефіцієнта кореляції Пірсона оцінимо щільність зв’язку між технічною швидкістю і продуктивністю праці. XY=5677,3 X=27,1 Y=209,4
Отже, коефіцієнт кореляції має значення: r =(5677,3-27,1*209,4)/(2,86*17,07)=+0,05, тому можна зробити висновок, що зв'язок є досить суттєвим, оскільки значення коефіцієнта кореляції є досить близьким до 1. Перевіримо істотність зв’язку між залишковою вартістю і кількістю їздок. К1=2-1=1 К2=24-2=22 Fф=0,0025/0,9975*22/1=0,06 Fкр=4,37 Таким чином, Fкр > Fф, що вказує на неістотність зв’язку між технічною швидкістю і продуктивністю праці.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 304. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

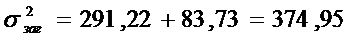
 -- таким чином маємо слабкий зв'язок між коефіцієнтом використання пробігу і продуктивністю праці, оскільки
-- таким чином маємо слабкий зв'язок між коефіцієнтом використання пробігу і продуктивністю праці, оскільки  .
. Для знаходження параметрів будується система рівняння:
Для знаходження параметрів будується система рівняння:

 ,
,
 З системи рівнянь отримуємо рівняння регресії:
З системи рівнянь отримуємо рівняння регресії: