
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эллипс и его характеристики.⇐ ПредыдущаяСтр 11 из 11 Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек Точки Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины
Рис. 7.1. Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Пусть
По определению эллипса
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим его:
Возведя обе части уравнения в квадрат и приведя подобные члены, получим:  Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем
Положительную величину
Оно называется каноническим уравнение эллипса. Координаты точек эллипса ограничены неравенствами
Заметим, что в уравнение (7.3) входят лишь четные степени Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
При возрастании
Рис. 7.4 Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
Оси симметрии эллипса (оси Если
Эксцентриситет
Фокальными радиусами точки Директрисы обладают следующим свойством: отношение расстояния Гипербола. Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек Точки Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:
где Уравнение (7.6) называется каноническим уравнением гиперболы. Из уравнения (7.6) видно, что Так как в уравнение входят только четные степени График этой функции от точки
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны

Рис 7.8. Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки Эксцентриситетом гиперболы называется число
Рис. 7.9 Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами Для правой - ветви Для левой - ветви Прямые 42.Парабола. Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки Для вывода канонического уравнения параболы ось В выбранной системе координат уравнение параболы имеет вид:
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что При неограниченном возрастании
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы. 42.Первообразная и неопределенный интеграл.Интегрирование – операция, обратная дифференцированию, которая позволяет определять функцию
Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной. Функция Теорема. Если Доказательство:
43. Основные свойства неопределенного интеграла.1.Производная неопределенного интеграла равна подынтегральной функцией:
1. Эти свойства означают, что интегрирование и дифференцирование – взаимно обратные операции. 2. Если 3. Если Таким образом, свойства 3 и 4 указывают на линейность операции интегрирования:
где
4. Если Таким образом, все семейство первообразных для данной функции Совокупность всех первообразных для функции Неопределенный интеграл обозначается следующим образом:
где
Таблица интегралов.
45.Метод подведения под знак дифференциала в неопределенном интеграле. Производная неопределенного интеграла равна подынтегральной функцией:
46.Метод подстановки. Для упрощения подынтегральной функции и, тем самым, для нахождения интеграла Если обозначить Для некоторых типов подынтегральных функций известны такие подстановки, которые приводят к цели. Ниже будут рассматриваться многие из них. Например: 1.
2.
3.
4. Наряду с заменой переменных часто применяется метод разложения, который опирается на линейные свойства интегралов. Это можно проиллюстрировать следующим примером: 5.
47.Интеграл, содержащий квадратный трехчлен.1. Интегрирование по частям. Если функции Действительно, если проинтегрировать формулу нахождения дифференциала произведения двух функций:
то можно получить следующее соотношение между первообразными от этих функций:
Такой способ нахождения интеграла называется интегрированием по частям. Этот способ целесообразно применять, если интеграл, стоящий в правой части проще исходного. При использовании метода интегрирования по частям задана левая часть равенства, т.е. функция Функции, интегрируемые по частям, можно схематично разделить на три группы. 1. Интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций:
В случае если подынтегральная функция содержит в качестве множителя одну из перечисленных выше функций в степени 2. Интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций:
Для вычисления интегралов второй группы нужно формулу интегрирования по частям применять 3. Интегралы вида:
Применение формулы интегрирования по частям может привести к ситуации, когда интеграл в правой части и интеграл в левой части равенства совпадают, т.е. получается равенство вида:
где
В этом случае применение метода интегрирования по частям позволяет получить уравнение первого порядка для
Причем, метод интегрирования по частям может применяться многократно и любой из сомножителей можно всякий раз принимать за Большое количество интегралов, не входящих в эти три группы, у которых невозможно выделить общий признак для группировки, также вычисляются методом интегрирования по частям. К таким интегралам можно отнести:
49. Интегрирование рациональных функций. Из курса линейной алгебры известно, что рациональной дробью называется выражение вида При интегрировании правильной рациональной дроби производится разложение этой дроби на простейшие, для чего предварительно разлагается на элементарные множители многочлен Интегралы вида · · Для вычисления интегралов вида ·
· Обозначим
Если ввести обозначение
Таким образом, происходит понижение порядка вычисляемого интеграла, и вычисление интеграла Зная с точностью до константы интеграл
Используя полученный результат, можно вычислить
Таким образом, можно вычислить интеграл 50.Интегрирование иррациональных функций. Если
приводится к интегралу от рациональной функции при помощи подстановки Сходная подстановка рационализирует подынтегральную функцию и в более общем случае интегрирования выражений типа:
В этом случае также применяется подстановка Вычисление Интеграл · Если · Если · Если то Здесь Интеграл Интеграл Интеграл Пример: Вычислить Применим подстановку Эйлера 51-52. Интегрирование тригонометрических функций. Интеграл
При вычислении таких интегралов можно использовать также и специальные подстановки, а именно: в случае, когда В случае неопределенного интеграла вида Если Если 53.Задачи, приводящие к понятию определенного интеграла. Интегральные суммы.Пусть функция Определение. Число
называется интегральной суммой (или суммой Римана) функции Геометрический смысл интегральной суммы – площадь ступенчатой фигуры.
Введем обозначение Определение. Число Определение.: Функция |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 242. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  есть величина постоянная (большая, чем расстояние между
есть величина постоянная (большая, чем расстояние между 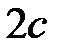 , а сумму расстояний от точек эллипса до фокусов через
, а сумму расстояний от точек эллипса до фокусов через  , имеем
, имеем  . Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
 походила через фокусы
походила через фокусы  к
к  , начало координат выберем в середине отрезка
, начало координат выберем в середине отрезка  и
и  .
. ‑ произвольная точка эллипса, тогда:
‑ произвольная точка эллипса, тогда: ,
, .
. . Подставляя сюда значения
. Подставляя сюда значения  и
и  , имеем:
, имеем:

 .
. или
или
 обозначим через
обозначим через  . Тогда уравнение (7.2) примет вид:
. Тогда уравнение (7.2) примет вид:
 . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами
. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами  и
и  :
: и
и 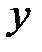 . Поэтому, если точка
. Поэтому, если точка  ,
,  ,
, 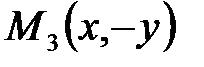 также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей
также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей  .
.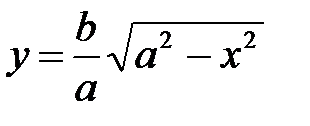
 от
от  до
до  ,
,  монотонно убывает от
монотонно убывает от 
 ) называются просто его осями, а центр симметрии – точка
) называются просто его осями, а центр симметрии – точка  ‑ центром эллипса. Точки
‑ центром эллипса. Точки  пересечения эллипса с осями координат называются вершинами эллипса. Отрезки
пересечения эллипса с осями координат называются вершинами эллипса. Отрезки  и
и  , а также их длины
, а также их длины  и
и  называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси
называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси  (как в нашем случае), из равенства
(как в нашем случае), из равенства  , следует, что
, следует, что  . В этом случае
. В этом случае  , то уравнение (7.3) можно переписать в виде:
, то уравнение (7.3) можно переписать в виде:
 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении  эллипса называются отрезки прямых, соединяющие эту точку с фокусами
эллипса называются отрезки прямых, соединяющие эту точку с фокусами  и
и  задаются формулами
задаются формулами  и
и  . Прямые
. Прямые  называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса  называется левой, а
называется левой, а 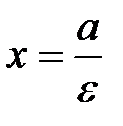 ‑ правой. Так как для эллипса
‑ правой. Так как для эллипса 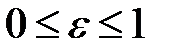 , то
, то 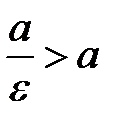 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины. любой точки эллипса от фокуса к ее расстоянию
любой точки эллипса от фокуса к ее расстоянию 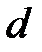 до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 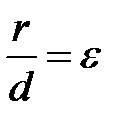 .
. . По условию,
. По условию,  .
.
 ‑ координаты произвольной точки гиперболы,
‑ координаты произвольной точки гиперболы,  .
. . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми
. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми 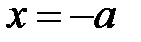 и
и  .
. и
и  , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:  .
. уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
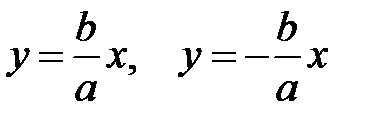 .
. и
и  параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
 и
и  пересечения гиперболы с осью
пересечения гиперболы с осью  и
и  называются полуосями гиперболы. Если
называются полуосями гиперболы. Если 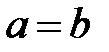 , то гипербола называется равносторонней.
, то гипербола называется равносторонней. . Для любой гиперболы
. Для любой гиперболы  . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси
. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси  . На рисунке 7.9 изображены гиперболы с различными значениями
. На рисунке 7.9 изображены гиперболы с различными значениями 
 и
и  ,
, .
.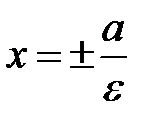 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением  .
. (фокуса) и данной прямой
(фокуса) и данной прямой  (директрисы).
(директрисы). перпендикулярно директрисе
перпендикулярно директрисе  пересечения оси
пересечения оси 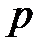 расстояние фокуса от директрисы, то
расстояние фокуса от директрисы, то  и уравнение директрисы будет иметь вид
и уравнение директрисы будет иметь вид  .
.
 может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси
может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси  . Так как уравнение (7.8) содержит
. Так как уравнение (7.8) содержит 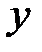 только в четной степени, то парабола симметрична относительно оси
только в четной степени, то парабола симметрична относительно оси  .
. . Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.
. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.
 , для которой заданная функция
, для которой заданная функция  является ее производной:
является ее производной: .
.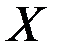 , если для каждой точки этого промежутка
, если для каждой точки этого промежутка  .
. и
и  – любые две первообразные для данной функции
– любые две первообразные для данной функции  выполняется равенство
выполняется равенство  .
. .
.

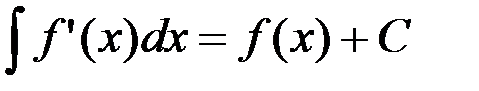
 – интегрируемые функции, т.е. на промежутке
– интегрируемые функции, т.е. на промежутке  они имеют первообразные, то сумма функций
они имеют первообразные, то сумма функций 
 .
. постоянная величина, то
постоянная величина, то  – также интегрируемая функция и
– также интегрируемая функция и  .
. ,
,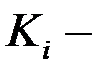 постоянные;
постоянные; интегрируемые функции.
интегрируемые функции. , а также
, а также  дифференцируемая функция, то
дифференцируемая функция, то 
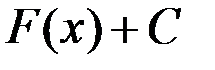 , где
, где  одна из первообразных, а
одна из первообразных, а  произвольная постоянная.
произвольная постоянная.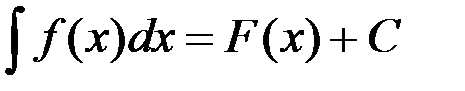 ,
, знак интеграла;
знак интеграла; подынтегральная функция;
подынтегральная функция; подынтегральное выражение.
подынтегральное выражение. ;
;
 ;
;
 ;
;
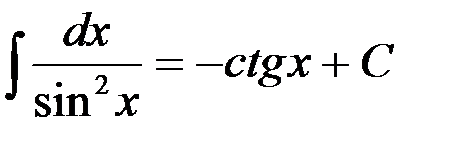 ;
;
 ;
;
 ;
;

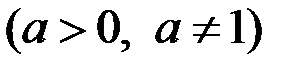 ;
;
 ;
;
 ;
;
 ;
;
 часто применяется так называемая подстановка или замена переменных.
часто применяется так называемая подстановка или замена переменных. и сделать соответствующие преобразования в заданном подынтегральном выражении, полученный интеграл при удачном выборе функции
и сделать соответствующие преобразования в заданном подынтегральном выражении, полученный интеграл при удачном выборе функции  может оказаться более простым или даже табличным.
может оказаться более простым или даже табличным. . Если применить замену
. Если применить замену  ;
;  , то получим:
, то получим: .
.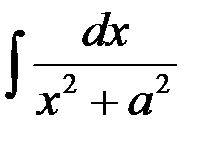 . Применим замену
. Применим замену  ;
;  . В результате получим:
. В результате получим: .
. Как и в предыдущем случае, применим замену
Как и в предыдущем случае, применим замену  .
. . Интегрирование этого выражения будет проведено позднее при подробном рассмотрении метода замены переменных.
. Интегрирование этого выражения будет проведено позднее при подробном рассмотрении метода замены переменных.
 .
. ,2.
,2.  ; 3.
; 3.  ; 4.
; 4. 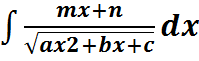 . Для их нахождения нужно 1)выделить полный квадрат двучлена, основание двучлена обозначить через t, а интегралы вида 1 и 3 –будут табличные, а 2 и 4 – следует разбить на сумму двух интегралов, один из которых будет табличным, а другой берется подстановкой или подведением под знак дифференциала.
. Для их нахождения нужно 1)выделить полный квадрат двучлена, основание двучлена обозначить через t, а интегралы вида 1 и 3 –будут табличные, а 2 и 4 – следует разбить на сумму двух интегралов, один из которых будет табличным, а другой берется подстановкой или подведением под знак дифференциала. и
и  дифференцируемы на множестве
дифференцируемы на множестве  , то на нем существует и интеграл
, то на нем существует и интеграл 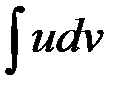 , причем
, причем  .
. ,
, . Таким образом, выбор функций
. Таким образом, выбор функций 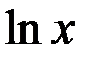 ,
, 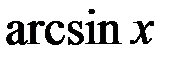 ,
,  ,
,  ,
,  ,
,  , при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.
, при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.
 , то операцию интегрирования по частям придется повторять
, то операцию интегрирования по частям придется повторять 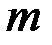 раз.
раз. ,
,  ,
,  , a также, полином
, a также, полином  й степени
й степени  :
: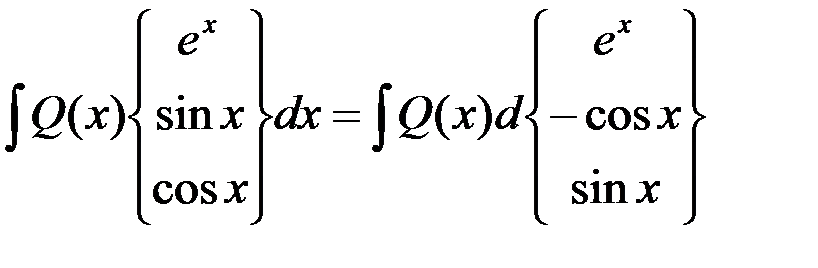 .
. раз, причем в качестве функции
раз, причем в качестве функции  ;
;  ;
;  .
. ,
, исходный интеграл;
исходный интеграл; постоянная
постоянная  .
. , из решения которого находится исходный интеграл
, из решения которого находится исходный интеграл  :
: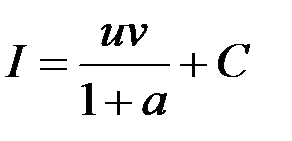 .
. ,
,  ,
,  ,
,  ,
, 
 , где
, где  и
и 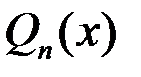 – многочлены степени
– многочлены степени  , соответственно. Рациональная дробь называется правильной при
, соответственно. Рациональная дробь называется правильной при  . В противном случае, когда
. В противном случае, когда  , рациональная дробь называется неправильной. Деление числителя на знаменатель позволяет от неправильной дроби перейти к правильной.
, рациональная дробь называется неправильной. Деление числителя на знаменатель позволяет от неправильной дроби перейти к правильной. и
и  .
.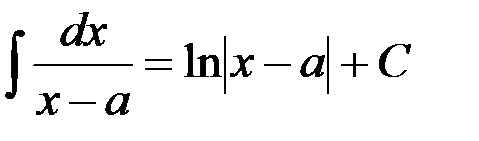 ;
; ;
;

 ;
;
 через
через  , тогда
, тогда  . Введем новую переменную
. Введем новую переменную 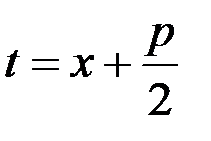 , тогда
, тогда  ,
,  .
.

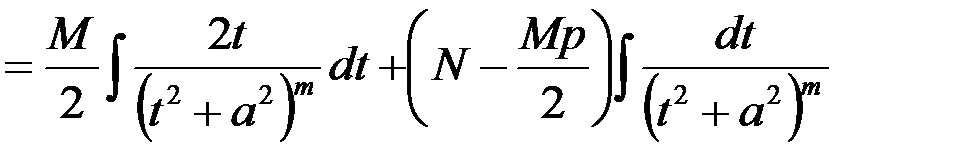 ;
;  .
.

 .
. , то полученное выражение можно переписать в следующем виде:
, то полученное выражение можно переписать в следующем виде:
 сводится к вычислению интеграла
сводится к вычислению интеграла  .
. можно вычислить
можно вычислить  :
: .
. :
:
 рациональная функция своих аргументов, а
рациональная функция своих аргументов, а  целые положительные числа, то интеграл:
целые положительные числа, то интеграл:
 , где
, где  наибольшее общее кратное показателей корней
наибольшее общее кратное показателей корней  .
. .
. , где, как и в рассмотренном выше случае,
, где, как и в рассмотренном выше случае,  .
.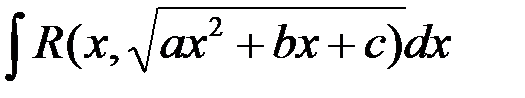
 сводится к интегралу от рациональной функции с помощью одной из следующих подстановок:
сводится к интегралу от рациональной функции с помощью одной из следующих подстановок: , то
, то  ;
; , то
, то  ;
; ,
,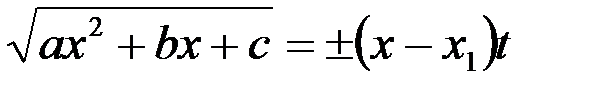 .
. - новая переменная.
- новая переменная.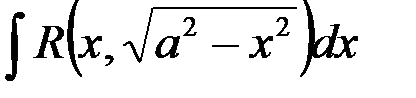 находится подстановкой
находится подстановкой  .
. находится подстановкой
находится подстановкой  .
. находится подстановкой
находится подстановкой  .
. .
.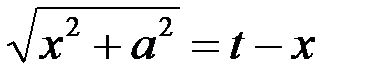 . Возводя это равенство почленно в квадрат, получим
. Возводя это равенство почленно в квадрат, получим  . Дифференцируя обе части полученного выражения, получим
. Дифференцируя обе части полученного выражения, получим  . Отсюда
. Отсюда  , или
, или  . Таким образом,
. Таким образом,  . Поскольку
. Поскольку  , то
, то  . Следовательно,
. Следовательно,  .
. , где
, где  - рациональная функция, всегда сводится к интегралу от рациональной функции при помощи универсальной подстановки
- рациональная функция, всегда сводится к интегралу от рациональной функции при помощи универсальной подстановки  . При этом:
. При этом: .
. , можно использовать подстановку
, можно использовать подстановку  .
. это соответствует нечетному значению
это соответствует нечетному значению  , можно использовать подстановку
, можно использовать подстановку  .
. , то можно использовать подстановку
, то можно использовать подстановку 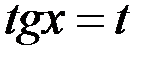 .
. ,
,  . Обозначим символом
. Обозначим символом  разбиение сегмента
разбиение сегмента  при помощи некоторых несовпадающих друг с другом точек
при помощи некоторых несовпадающих друг с другом точек  на
на  частичных сегментов
частичных сегментов  ,
,  ,
,  ,
,  . Точки
. Точки  ,
,  ,
,  ,
, 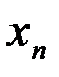 будем называть точками разбиения
будем называть точками разбиения  . Пусть
. Пусть  - произвольная точка частичного сегмента
- произвольная точка частичного сегмента  , а
, а  - разность
- разность  , которую мы в дальнейшем будем называть длиной частичного сегмента
, которую мы в дальнейшем будем называть длиной частичного сегмента  .
. , где:
, где:
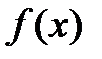 , соответствующей разбиению
, соответствующей разбиению 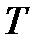 сегмента
сегмента  и данному выбору промежуточных точек
и данному выбору промежуточных точек  на частичных сегментах
на частичных сегментах  .
.
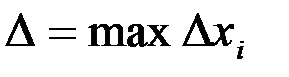 .
. при
при  , если для любого положительного
, если для любого положительного  можно указать такое число
можно указать такое число  , что для любого разбиения
, что для любого разбиения  частичных сегментов меньше
частичных сегментов меньше  , независимо от выбора точек
, независимо от выбора точек  , на сегментах
, на сегментах  выполняется неравенство
выполняется неравенство  , т.е.
, т.е.  .
. интегральных сумм этой функции при
интегральных сумм этой функции при  . Указанный предел
. Указанный предел