Основные прав ила дифференцирования.
1. Функция 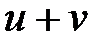 дифференцируема и дифференцируема и  ; ;
2. Если 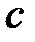 ‑ постоянная, то функция ‑ постоянная, то функция 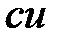 дифференцируема и дифференцируема и 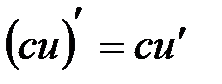 ; ;
3. Из 1 и 2 следует, что  ; ;
4. Функция 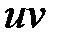 дифференцируема и дифференцируема и 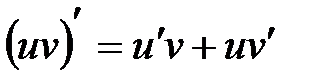 ; ;
5. Из 4 следует, что 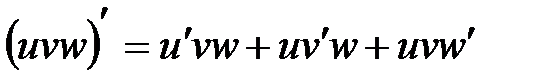 ; ;
6. Если 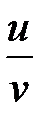 определена и дифференцируема, то определена и дифференцируема, то 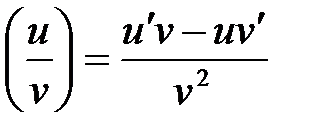 . .
28.Производная сложной и обратной функции. Производная сложной функции. Пусть 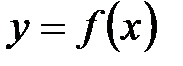 и и 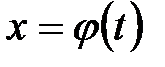 . Тогда можно определить сложную функцию . Тогда можно определить сложную функцию 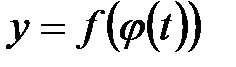 . Если функция . Если функция 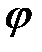 дифференцируема в точке дифференцируема в точке 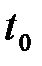 , а функция , а функция 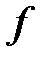 дифференцируема в точке дифференцируема в точке 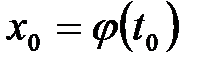 , то сложная функция , то сложная функция 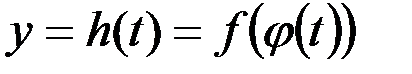 дифференцируема в точке дифференцируема в точке  , и ее производная может быть вычислена по правилу цепочки: , и ее производная может быть вычислена по правилу цепочки:
 . .
Или более кратко 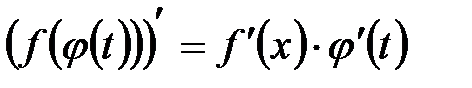 . .
Правило можно записать также в виде: 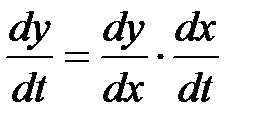 . .
Производная обратной функции
Пусть функция 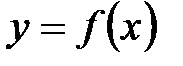 задана на множестве задана на множестве 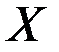 , а , а 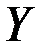 – множество ее значений. Тогда каждому – множество ее значений. Тогда каждому  ставится в соответствие единственное значение ставится в соответствие единственное значение 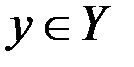 . С другой стороны, каждому . С другой стороны, каждому 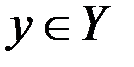 будет соответствовать одно или несколько значений будет соответствовать одно или несколько значений  . В случае, когда отображение . В случае, когда отображение 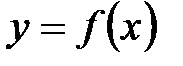 является биективным, т.е. каждому значению является биективным, т.е. каждому значению 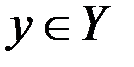 соответствует только одно значение соответствует только одно значение  , для которого , для которого  , на множестве , на множестве 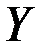 можно определить функцию можно определить функцию 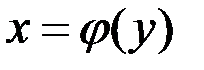 , множеством значений которой является , множеством значений которой является 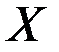 , которая будет называться обратной по отношению к функции , которая будет называться обратной по отношению к функции  . Функции . Функции 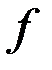 и и 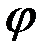 называются взаимообратными. называются взаимообратными.
Пусть функция 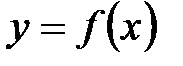 удовлетворяет условиям существования обратной функции и в точке удовлетворяет условиям существования обратной функции и в точке 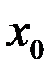 имеет конечную производную имеет конечную производную 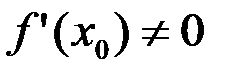 . Тогда обратная функция . Тогда обратная функция 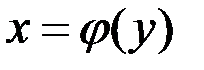 в точке в точке 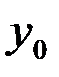 также имеет конечную производную, равную также имеет конечную производную, равную 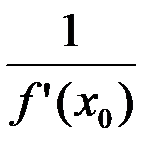 . .
Дифференциал функции и его основные свойства.
Дифференцируемость функции 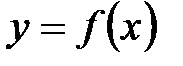 в точке в точке 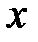 означает, что ее приращение представимо в виде: означает, что ее приращение представимо в виде:
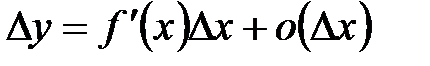 . .
Величина 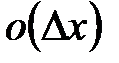 при малых при малых 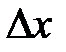 мала по сравнению с величиной мала по сравнению с величиной 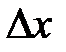 . Поэтому . Поэтому 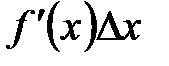 представляет собой главную часть приращения представляет собой главную часть приращения 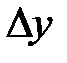 , называемую дифференциалом функции в точке , называемую дифференциалом функции в точке  . Дифференциал функции . Дифференциал функции 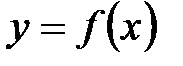 обозначают обычно символами: обозначают обычно символами: 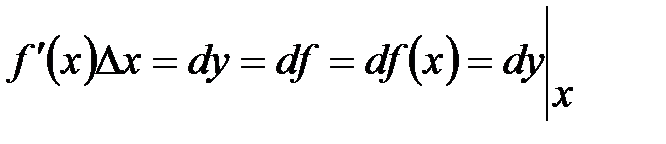 и др. и др.
Если  ‑ независимая переменная, то ‑ независимая переменная, то  и поэтому и поэтому 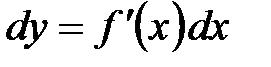 . .
Вычисление дифференциалов проводят по правилам 1 ‑ 6 дифференцирования с заменой символа ¢ (штрих) на символ 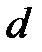 . Например: . Например:
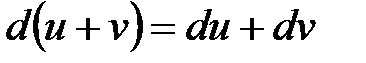 ; ;
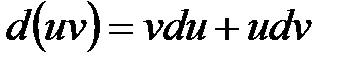 . .
Таким образом, приращение функции 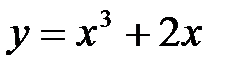 в точке в точке 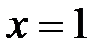 при малых значениях при малых значениях 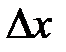 приблизительно в пять раз больше, чем приблизительно в пять раз больше, чем 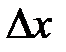 , а приращение функции в точке , а приращение функции в точке  приблизительно в 14 раз больше, чем приблизительно в 14 раз больше, чем 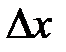 . .
Теоремы о дифференцируемых функциях.
Теорема Ферма. Если функция 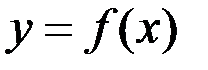 дифференцируема в точке дифференцируема в точке  , т.е. существует , т.е. существует  , и всюду в некоторой окрестности этой точки , и всюду в некоторой окрестности этой точки 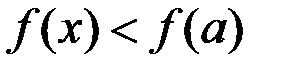  , т.е. , т.е. 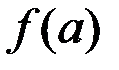 является наибольшим (наименьшим) значением функции в этой окрестности, то является наибольшим (наименьшим) значением функции в этой окрестности, то 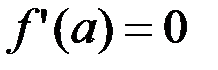 . .
Теорема Ролля. Если функция 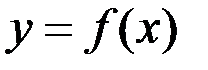 непрерывна на отрезке непрерывна на отрезке 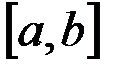 , дифференцируема на интервале , дифференцируема на интервале  и и 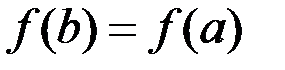 , то в некоторой точке интервала , то в некоторой точке интервала 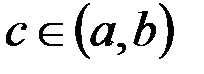 ее производная равна нулю. ее производная равна нулю.
Геометрический смысл теоремы Ролля заключается в том, что в  найдется точка, в которой касательная к кривой будет горизонтальна. найдется точка, в которой касательная к кривой будет горизонтальна.
Теорема Лагранжа. Если функция 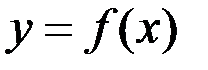 непрерывна на отрезке непрерывна на отрезке 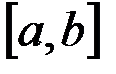 , дифференцируема на интервале , дифференцируема на интервале 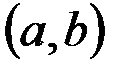 , то найдется точка , то найдется точка  для которой для которой 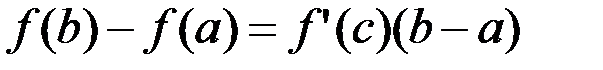 . .
Следствие. Теорема Лагранжа является обобщением теоремы Ролля для случая 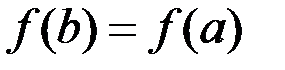 . Тогда . Тогда 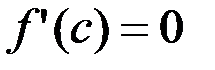 . .
Теорема Коши. Если функции  и и 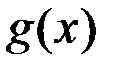 определены и непрерывны на отрезке определены и непрерывны на отрезке 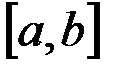 , дифференцируемы на интервале , дифференцируемы на интервале  и при этом и при этом 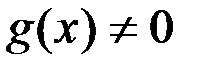 , то найдется точка , то найдется точка  , для которой , для которой 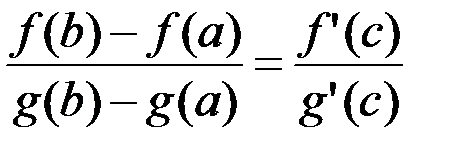 . .
Правило Лопиталя.
Пусть 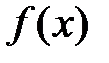 и и 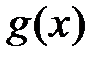 - функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или - функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или 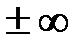 (если (если 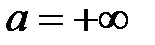 , то под окрестностью точки a понимаем какой-нибудь луч , то под окрестностью точки a понимаем какой-нибудь луч 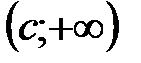 ; если ; если  , то окрестность – луч , то окрестность – луч 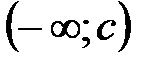 ). В самой точке a функции могут быть не определены. Пусть ). В самой точке a функции могут быть не определены. Пусть 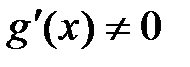 при при  . .
I правило. Если:
1. 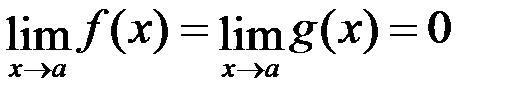
2. Существует конечный или бесконечный предел 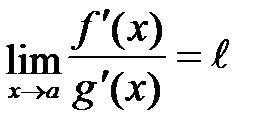 . Тогда: . Тогда: 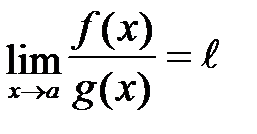 . .
II правило. Если:
1.  ; ;
2. Существует конечный или бесконечный предел 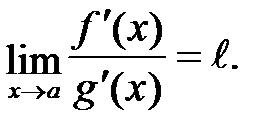 Тогда: Тогда: 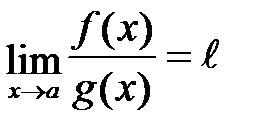 . .
Правила Лопиталя позволяют раскрывать неопределенности вида 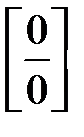 или или  . Однако, они могут быть использованы и при раскрытии неопределенностей других видов: . Однако, они могут быть использованы и при раскрытии неопределенностей других видов: 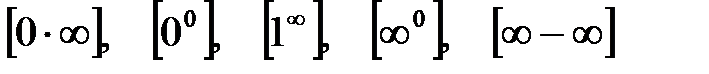 . Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида . Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида 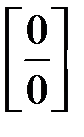 или или 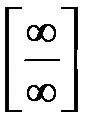 . .
32.Исследование на монотонность. Точки экстремума. . Функция 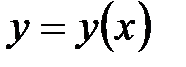 называется возрастающей на промежутке называется возрастающей на промежутке 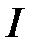 , если , если 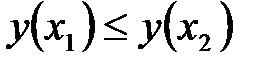 для любых точек для любых точек 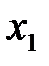 и и 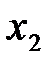 из промежутка из промежутка 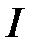 , удовлетворяющих неравенству , удовлетворяющих неравенству 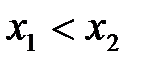 . Функция называется убывающей на . Функция называется убывающей на 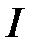 , если из условия , если из условия 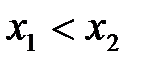 следует следует 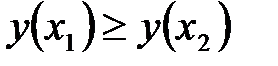 . .
Теорема. Если функция 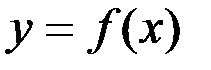 непрерывна на отрезке непрерывна на отрезке 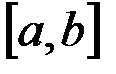 , дифференцируема на интервале , дифференцируема на интервале 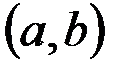 , то для того, чтобы , то для того, чтобы 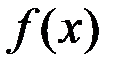 была возрастающей (убывающей) необходимо и достаточно, чтобы была возрастающей (убывающей) необходимо и достаточно, чтобы 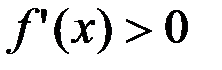  в каждой внутренней точке интервала в каждой внутренней точке интервала 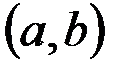 . .
Дифференцируемая функция является возрастающей на промежутке 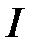 тогда и только тогда, когда тогда и только тогда, когда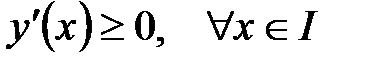 . .
Локальный экстремум
Точка 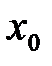 называется точкой локального максимума функции называется точкой локального максимума функции 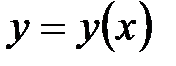 , если существует интервал , если существует интервал 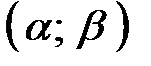 , содержащий точку , содержащий точку 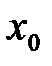 такой что такой что 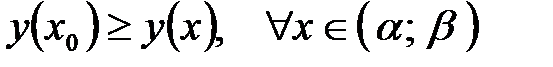 . .
Точка 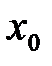 называется точкой локального минимума функции называется точкой локального минимума функции 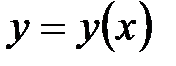 , если существует интервал , если существует интервал 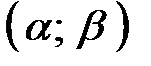 , содержащий точку , содержащий точку 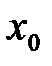 такой что такой что 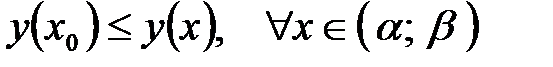 . .
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства  . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение: . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:  . .
Решения этого уравнения называют стационарными точками.
Исследование стационарных точек
I правило. Если при возрастании  при переходе через стационарную точку при переходе через стационарную точку 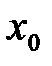 производная производная 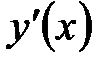 меняет знак с + на ‑ , то меняет знак с + на ‑ , то
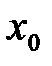 ‑ точка локального максимума. Если ‑ точка локального максимума. Если 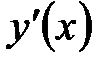 меняет знак с ‑ на + , то меняет знак с ‑ на + , то 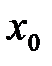 ‑ точка локального минимума функции ‑ точка локального минимума функции 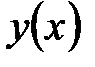 . Если . Если 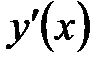 не меняет знак в точке не меняет знак в точке 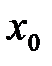 , то экстремума нет. , то экстремума нет.
II правило. Если вторая производная 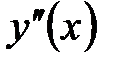 в стационарной точке в стационарной точке 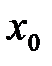 положительная, то положительная, то 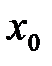 ‑ точка локального минимума функции ‑ точка локального минимума функции 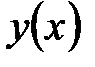 . Если вторая производная . Если вторая производная 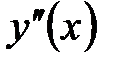 в стационарной точке в стационарной точке 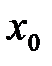 отрицательная, то отрицательная, то 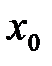 ‑ точка локального максимума функции ‑ точка локального максимума функции 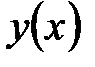 . .
Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.
Глобальный экстремум.Непрерывная на отрезке 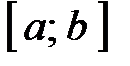 функция функция 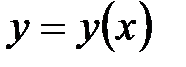 принимает свое наибольшее значение принимает свое наибольшее значение 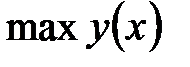 и свое наименьшее значение и свое наименьшее значение 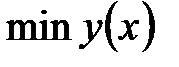 в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений 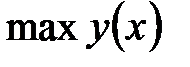 и и 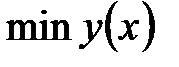 поступают следующим образом. поступают следующим образом.
· Находят стационарные точки  функции; функции;
· Находят точки  , в которых производная , в которых производная 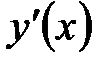 не существует или обращается в бесконечность; не существует или обращается в бесконечность;
· Вычисляют значения:
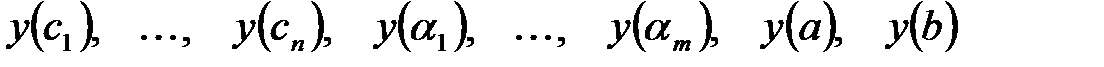 ‑ и выбирают среди этих чисел наибольшее и наименьшее. ‑ и выбирают среди этих чисел наибольшее и наименьшее.
Это и будут 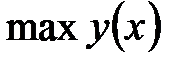 и и 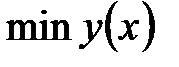 ‑ глобальные экстремальные значения. ‑ глобальные экстремальные значения.
33.Выпуклость, вогнутость. Точки перегиба. Графиком функции  , заданной на множестве , заданной на множестве 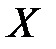 , называют множество точек плоскости с координатами , называют множество точек плоскости с координатами 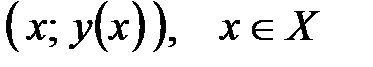 . График называют выпуклым вниз на промежутке . График называют выпуклым вниз на промежутке 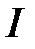 , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба. , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
Если на промежутке 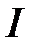 вторая производная вторая производная 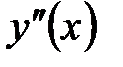 положительна, то график является выпуклым вниз на этом промежутке. Если положительна, то график является выпуклым вниз на этом промежутке. Если 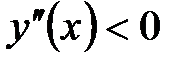 на промежутке на промежутке 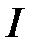 , то график является выпуклым вверх на промежутке , то график является выпуклым вверх на промежутке 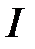 . .
Точка 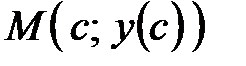 может быть точкой перегиба только в том случае, когда может быть точкой перегиба только в том случае, когда 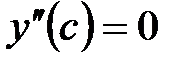 , либо , либо 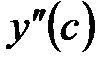 не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке 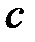 не означает еще, что в точке не означает еще, что в точке 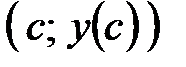 будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки. будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
I правило. Если  равна нулю или не существует и равна нулю или не существует и 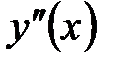 при переводе через точку при переводе через точку 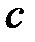 меняет знак, то меняет знак, то 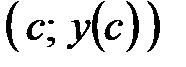 ‑ точка перегиба графика функции ‑ точка перегиба графика функции  . .
II правило. Если 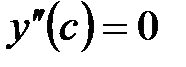 и и 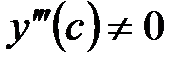 , то , то 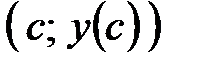 является точкой перегиба графика функции является точкой перегиба графика функции 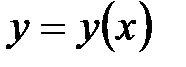 . .
34.Ассимптоты. Находят точки разрыва и промежутки, на которых она непрерывна. Выясняют характер точек разрыва. Вычисляют предельные значения функции в граничных точках множества  (если таковые имеются). Находят вертикальные асимптоты (если таковые имеются). Находят вертикальные асимптоты
(в точках бесконечного скачка). Если 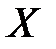 не ограничено, то вычисляют пределы функции при не ограничено, то вычисляют пределы функции при 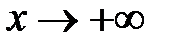 и и 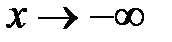 . Если . Если 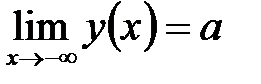 , то график имеет горизонтальную левостороннюю асимптоту , то график имеет горизонтальную левостороннюю асимптоту 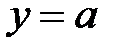 , если , если 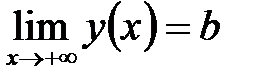 , график имеет горизонтальную правостороннюю асимптоту , график имеет горизонтальную правостороннюю асимптоту 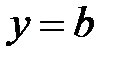 . Если пределы (или один из пределов) бесконечны, то график может иметь наклонные (левостороннюю и правостороннюю) асимптоты . Если пределы (или один из пределов) бесконечны, то график может иметь наклонные (левостороннюю и правостороннюю) асимптоты 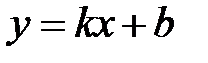 . Коэффициенты левосторонней асимптоты можно найти по формулам: . Коэффициенты левосторонней асимптоты можно найти по формулам:
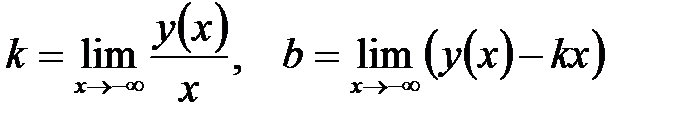 . .
Аналогично находят коэффициенты правосторонней асимптоты (нужно вычислить пределы при 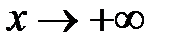 ). ).
Вычисляют производную 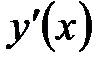 . Находят критические точки функции . Находят критические точки функции 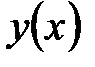 , т.е. стационарные точки и точки, в которых , т.е. стационарные точки и точки, в которых 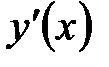 не существует. Выделяют промежутки, на которых не существует. Выделяют промежутки, на которых 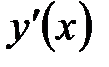 сохраняет знак. Это позволяет исследовать монотонность функции сохраняет знак. Это позволяет исследовать монотонность функции 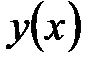 . .
|


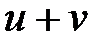 дифференцируема и
дифференцируема и  ;
;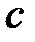 ‑ постоянная, то функция
‑ постоянная, то функция 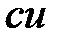 дифференцируема и
дифференцируема и 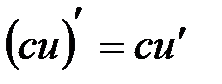 ;
; ;
;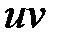 дифференцируема и
дифференцируема и 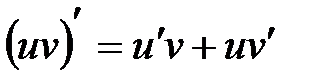 ;
;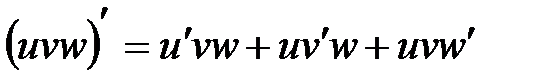 ;
;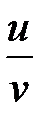 определена и дифференцируема, то
определена и дифференцируема, то 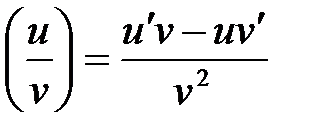 .
.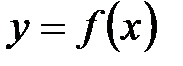 и
и 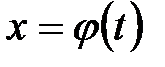 . Тогда можно определить сложную функцию
. Тогда можно определить сложную функцию 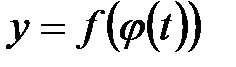 . Если функция
. Если функция 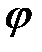 дифференцируема в точке
дифференцируема в точке 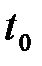 , а функция
, а функция 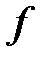 дифференцируема в точке
дифференцируема в точке 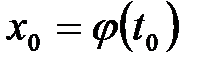 , то сложная функция
, то сложная функция 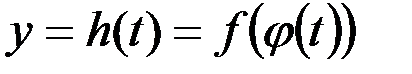 дифференцируема в точке
дифференцируема в точке  , и ее производная может быть вычислена по правилу цепочки:
, и ее производная может быть вычислена по правилу цепочки: .
.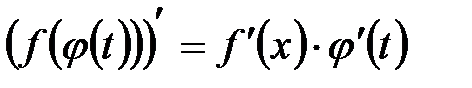 .
.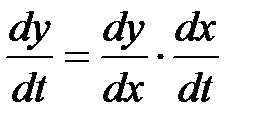 .
.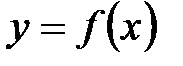 задана на множестве
задана на множестве 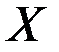 , а
, а 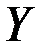 – множество ее значений. Тогда каждому
– множество ее значений. Тогда каждому  ставится в соответствие единственное значение
ставится в соответствие единственное значение 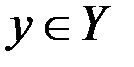 . С другой стороны, каждому
. С другой стороны, каждому 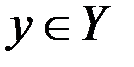 будет соответствовать одно или несколько значений
будет соответствовать одно или несколько значений  , на множестве
, на множестве 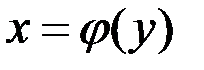 , множеством значений которой является
, множеством значений которой является 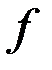 и
и 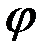 называются взаимообратными.
называются взаимообратными.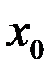 имеет конечную производную
имеет конечную производную 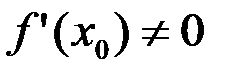 . Тогда обратная функция
. Тогда обратная функция 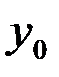 также имеет конечную производную, равную
также имеет конечную производную, равную 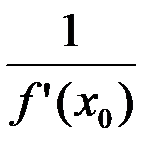 .
.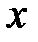 означает, что ее приращение представимо в виде:
означает, что ее приращение представимо в виде: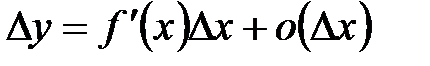 .
.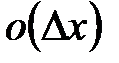 при малых
при малых 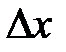 мала по сравнению с величиной
мала по сравнению с величиной 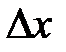 . Поэтому
. Поэтому 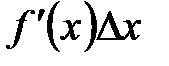 представляет собой главную часть приращения
представляет собой главную часть приращения 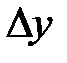 , называемую дифференциалом функции в точке
, называемую дифференциалом функции в точке  . Дифференциал функции
. Дифференциал функции 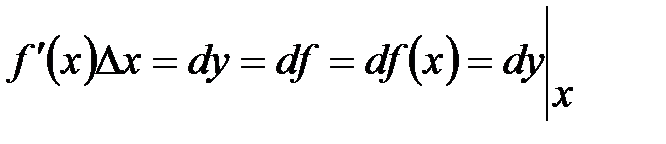 и др.
и др. и поэтому
и поэтому 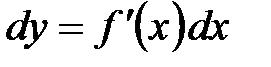 .
.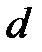 . Например:
. Например: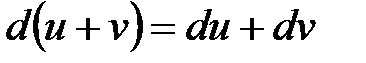 ;
;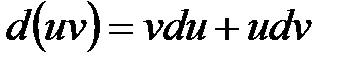 .
.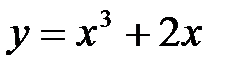 в точке
в точке 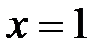 при малых значениях
при малых значениях 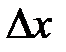 приблизительно в пять раз больше, чем
приблизительно в пять раз больше, чем  приблизительно в 14 раз больше, чем
приблизительно в 14 раз больше, чем 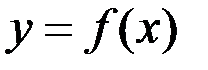 дифференцируема в точке
дифференцируема в точке  , т.е. существует
, т.е. существует  , и всюду в некоторой окрестности этой точки
, и всюду в некоторой окрестности этой точки 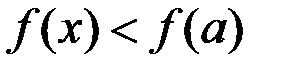
 , т.е.
, т.е. 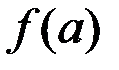 является наибольшим (наименьшим) значением функции в этой окрестности, то
является наибольшим (наименьшим) значением функции в этой окрестности, то 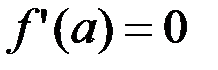 .
.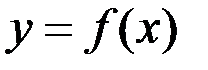 непрерывна на отрезке
непрерывна на отрезке 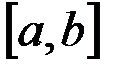 , дифференцируема на интервале
, дифференцируема на интервале  и
и 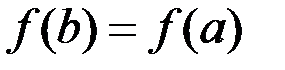 , то в некоторой точке интервала
, то в некоторой точке интервала 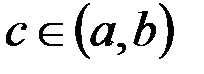 ее производная равна нулю.
ее производная равна нулю.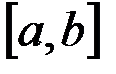 , дифференцируема на интервале
, дифференцируема на интервале 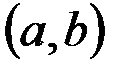 , то найдется точка
, то найдется точка  для которой
для которой 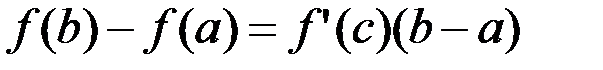 .
.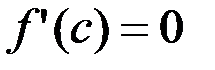 .
. и
и 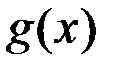 определены и непрерывны на отрезке
определены и непрерывны на отрезке 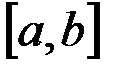 , дифференцируемы на интервале
, дифференцируемы на интервале 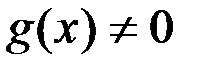 , то найдется точка
, то найдется точка 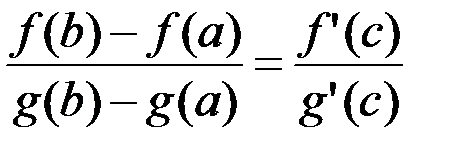 .
.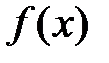 и
и 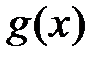 - функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или
- функции, определенные и дифференцируемые в окрестности точки a, где a - конечное число или 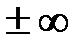 (если
(если 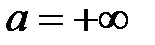 , то под окрестностью точки a понимаем какой-нибудь луч
, то под окрестностью точки a понимаем какой-нибудь луч 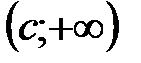 ; если
; если  , то окрестность – луч
, то окрестность – луч 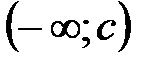 ). В самой точке a функции могут быть не определены. Пусть
). В самой точке a функции могут быть не определены. Пусть 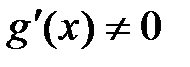 при
при  .
.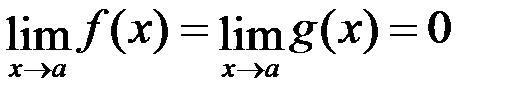
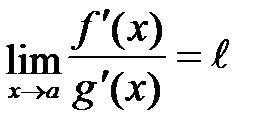 . Тогда:
. Тогда: 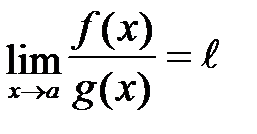 .
. ;
;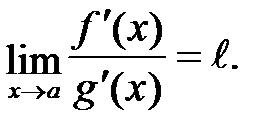 Тогда:
Тогда: 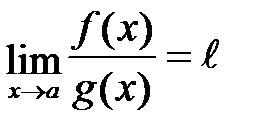 .
.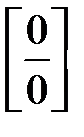 или
или  . Однако, они могут быть использованы и при раскрытии неопределенностей других видов:
. Однако, они могут быть использованы и при раскрытии неопределенностей других видов: 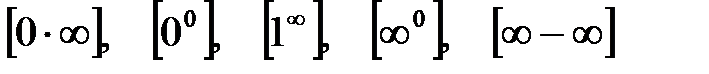 . Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида
. Для этого исследуемое выражение преобразуют так, чтобы получилась неопределенность вида 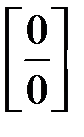 или
или  .
.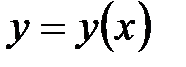 называется возрастающей на промежутке
называется возрастающей на промежутке 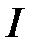 , если
, если 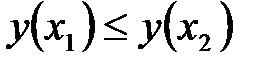 для любых точек
для любых точек 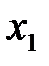 и
и 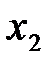 из промежутка
из промежутка 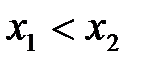 . Функция называется убывающей на
. Функция называется убывающей на 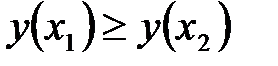 .
.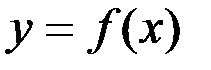 непрерывна на отрезке
непрерывна на отрезке 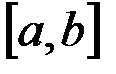 , дифференцируема на интервале
, дифференцируема на интервале 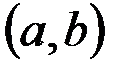 , то для того, чтобы
, то для того, чтобы 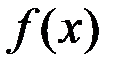 была возрастающей (убывающей) необходимо и достаточно, чтобы
была возрастающей (убывающей) необходимо и достаточно, чтобы 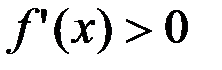
 в каждой внутренней точке интервала
в каждой внутренней точке интервала 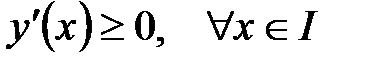 .
.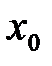 называется точкой локального максимума функции
называется точкой локального максимума функции 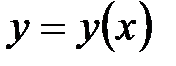 , если существует интервал
, если существует интервал 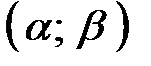 , содержащий точку
, содержащий точку 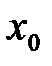 такой что
такой что 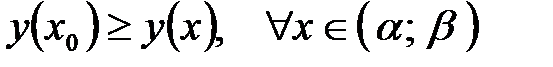 .
.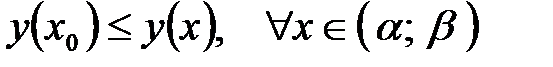 .
. . Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение:
. Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение: 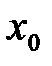 производная
производная 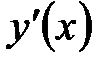 меняет знак с + на ‑ , то
меняет знак с + на ‑ , то 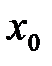 ‑ точка локального минимума функции
‑ точка локального минимума функции 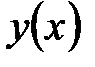 . Если
. Если 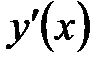 не меняет знак в точке
не меняет знак в точке 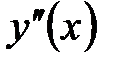 в стационарной точке
в стационарной точке 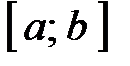 функция
функция 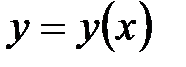 принимает свое наибольшее значение
принимает свое наибольшее значение 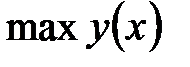 и свое наименьшее значение
и свое наименьшее значение 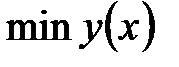 в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений
в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений  функции;
функции; , в которых производная
, в которых производная 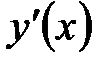 не существует или обращается в бесконечность;
не существует или обращается в бесконечность;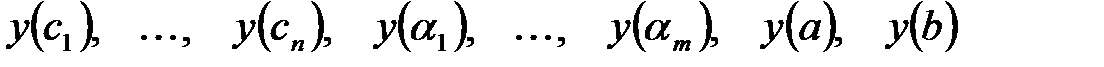 ‑ и выбирают среди этих чисел наибольшее и наименьшее.
‑ и выбирают среди этих чисел наибольшее и наименьшее.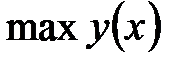 и
и  , заданной на множестве
, заданной на множестве 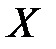 , называют множество точек плоскости с координатами
, называют множество точек плоскости с координатами 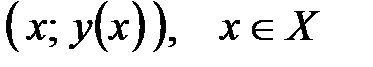 . График называют выпуклым вниз на промежутке
. График называют выпуклым вниз на промежутке 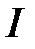 , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
, если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.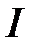 вторая производная
вторая производная 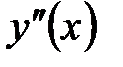 положительна, то график является выпуклым вниз на этом промежутке. Если
положительна, то график является выпуклым вниз на этом промежутке. Если 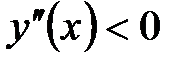 на промежутке
на промежутке 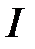 .
.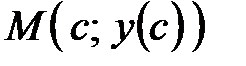 может быть точкой перегиба только в том случае, когда
может быть точкой перегиба только в том случае, когда 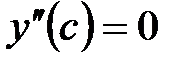 , либо
, либо 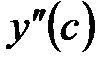 не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке
не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке 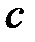 не означает еще, что в точке
не означает еще, что в точке 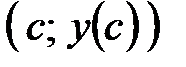 будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки. равна нулю или не существует и
равна нулю или не существует и 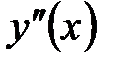 при переводе через точку
при переводе через точку 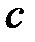 меняет знак, то
меняет знак, то 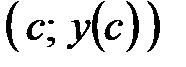 ‑ точка перегиба графика функции
‑ точка перегиба графика функции  .
.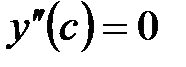 и
и 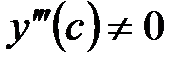 , то
, то 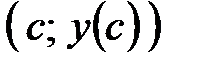 является точкой перегиба графика функции
является точкой перегиба графика функции 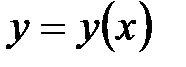 .
. (если таковые имеются). Находят вертикальные асимптоты
(если таковые имеются). Находят вертикальные асимптоты 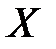 не ограничено, то вычисляют пределы функции при
не ограничено, то вычисляют пределы функции при 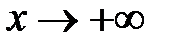 и
и 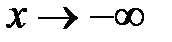 . Если
. Если 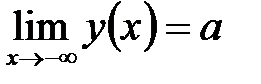 , то график имеет горизонтальную левостороннюю асимптоту
, то график имеет горизонтальную левостороннюю асимптоту 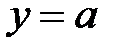 , если
, если 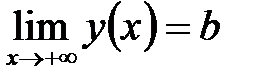 , график имеет горизонтальную правостороннюю асимптоту
, график имеет горизонтальную правостороннюю асимптоту 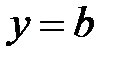 . Если пределы (или один из пределов) бесконечны, то график может иметь наклонные (левостороннюю и правостороннюю) асимптоты
. Если пределы (или один из пределов) бесконечны, то график может иметь наклонные (левостороннюю и правостороннюю) асимптоты 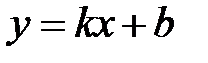 . Коэффициенты левосторонней асимптоты можно найти по формулам:
. Коэффициенты левосторонней асимптоты можно найти по формулам: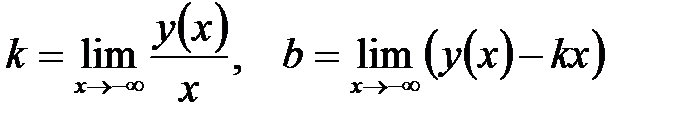 .
.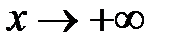 ).
).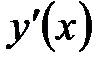 . Находят критические точки функции
. Находят критические точки функции 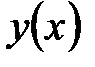 , т.е. стационарные точки и точки, в которых
, т.е. стационарные точки и точки, в которых 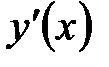 не существует. Выделяют промежутки, на которых
не существует. Выделяют промежутки, на которых 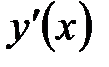 сохраняет знак. Это позволяет исследовать монотонность функции
сохраняет знак. Это позволяет исследовать монотонность функции 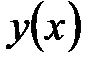 .
.