
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Смешанное произведение векторов.Смешанным произведением тройки векторов Таким образом, смешанное произведение векторов Знак произведение положителен, если векторы Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов Если
или в свернутой форме:
Справедливы следующие свойства смешанного произведения векторов: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей 2. При перестановке двух соседних множителей смешанное произведение меняет свой знак на противоположный Функция. Основные понятия. Пусть  Множество Существуют аналитический, графический, табличный и др. способы задания функции. При аналитическом способе зависимость между переменными определяется формулами. Если при этом множество При графическом способе задания функции зависимость между переменными отражается с помощью графика. Графиком функции на плоскости При табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции. Таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно при решении интерполяционной задачи. Поэтому в общем случае найти точное аналитическое выражение функции по ее табличным данным нельзя. Однако всегда можно построить интерполяционную формулу, и притом не одну (например, многочлен Лагранжа), которая для значений аргумента, имеющихся в таблице, будет давать соответствующие табличные значения функции. Функции характеризуются рядом свойств, к важнейшим из которых относятся: четность, нули, периодичность, ограниченность, монотонность функции, а также наличие у функции асимптот и обратной функции: · Функция · Функция · Нулями функции · Функция · Функция · Асимптотой графика функции называется прямая, к которой сколь угодно близко приближается график данной функции при стремлении аргумента к бесконечности (горизонтальная и наклонная асимптоты), или к некоторому числу · Функция · Функция · Если каждому значению переменной |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 239. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 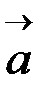 на векторное произведение
на векторное произведение  . Если рассматриваемые векторы
. Если рассматриваемые векторы  есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор
есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор  , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов
, то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов  (которое обозначается
(которое обозначается  ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах  направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от  к
к  виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки.
 , и
, и  , то:
, то: ,
, .
.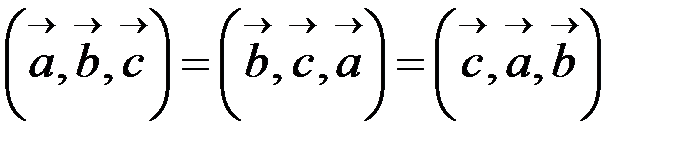 ;
; .
. ‑ некоторое числовое множество и пусть задан закон (правило)
‑ некоторое числовое множество и пусть задан закон (правило)  , по которому каждому числу
, по которому каждому числу  ставится в соответствие единственное число
ставится в соответствие единственное число  , обозначаемое
, обозначаемое  . Тогда говорят, что на множестве
. Тогда говорят, что на множестве  задана функция
задана функция  или
или  Чаще используют более простую терминологию: задана функция
Чаще используют более простую терминологию: задана функция  ,
,  .
. называют множеством значений функции
называют множеством значений функции  . При этом
. При этом  называют независимой переменной или аргументом функции,
называют независимой переменной или аргументом функции,  – зависимой переменной или значением функции, а
– зависимой переменной или значением функции, а  ,
,  ,
,  ,
,  и т.д.). Частное значение функции
и т.д.). Частное значение функции  при
при  записывается как
записывается как  .
. называется геометрическое место точек
называется геометрическое место точек  , координаты которых связаны функциональной зависимостью.
, координаты которых связаны функциональной зависимостью. называется четной, если для любого значения ее аргумента из области определения выполняется равенство
называется четной, если для любого значения ее аргумента из области определения выполняется равенство  . Сумма, разность и произведение четных функций есть функция четная;
. Сумма, разность и произведение четных функций есть функция четная; называется нечетной, если для любого значения аргумента из области ее определения выполняется равенство
называется нечетной, если для любого значения аргумента из области ее определения выполняется равенство  . Сумма и разность нечетных функций есть функция нечетная, а частное и произведение нечетных функций – функция четная;
. Сумма и разность нечетных функций есть функция нечетная, а частное и произведение нечетных функций – функция четная; называют значения аргумента, при которых функция обращается в ноль. Графически нулями функции являются точки пересечения графика функции с осью абсцисс;
называют значения аргумента, при которых функция обращается в ноль. Графически нулями функции являются точки пересечения графика функции с осью абсцисс; называется периодической, если существует число
называется периодической, если существует число  такое, что для каждого значения аргумента
такое, что для каждого значения аргумента  из области ее определения выполняется равенство
из области ее определения выполняется равенство  . Число
. Число  называют периодом этой функции;
называют периодом этой функции; называется возрастающей на некотором промежутке, если для любых значений
называется возрастающей на некотором промежутке, если для любых значений  . Функция
. Функция  называется убывающей на некотором промежутке, если для любых значений
называется убывающей на некотором промежутке, если для любых значений  . Как возрастающие, так и убывающие функции называются монотонными;
. Как возрастающие, так и убывающие функции называются монотонными; (вертикальная асимптота);
(вертикальная асимптота); называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число  такое, что для каждого значения аргумента
такое, что для каждого значения аргумента  . Функция
. Функция  называется ограниченной, если существует число
называется ограниченной, если существует число  такое, что для каждого значения аргумента
такое, что для каждого значения аргумента  ;
; называется обратной по отношению к
называется обратной по отношению к  , если при подстановке её вместо аргумента
, если при подстановке её вместо аргумента  ;
; , то
, то  называется однозначной функцией от
называется однозначной функцией от  называется многозначной (двузначной, трехзначной и т.д.) функцией от
называется многозначной (двузначной, трехзначной и т.д.) функцией от