
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные операции над векторами.Стр 1 из 11Следующая ⇒ Действия над матрицами. Суммой двух матриц Сложение матриц обладает следующими свойствами: Коммутативность, т.е. Ассоциативность, т.е. Для любых двух матриц Произведением матрицы Умножение матрицы на действительное число обладает следующими свойствами:
Матрица Свойства умножения: Если матрица
Умножение матриц не коммутативно, т.е., как правило, Обратная матрица. Пример. Пусть  Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.Пусть
здесь 4.Теорема Кронекеля-Копеля.?Ответ о совместимости системы линейных ур-ний дает теорема Кронекеля-Конеля.Система совместима тогда и только тогда когда ранг матрицы А =рангу матрицы 5.Векторы.Основные понятия.Скалярной величиной или скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, цена, количество проданного товара, стоимость и т.д.Векторной величиной или вектором называется величина, для задания которой кроме численного значения необходимо указать и ее направление в пространстве, например, изменение темпов производства (рост или падение), колебание курса акций на бирже и т.д.Векторная величина графически обычно изображается как связанный вектор или направленный отрезок, т.е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление, свободный вектор или просто вектор представляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется: направлением;длиной (модулем). Для задания такого множества достаточно указать какой-либо один из связанных векторов этого множества – представитель вектора, в качестве которого обычно выбирается связанный вектор с началом, совпадающим с началом координат.Вектор обозначается одной маленькой буквой со стрелкой сверху, например, Длина вектора называется его модулем, обозначается Два вектора называются равными, если: 1. равны их длины; 2. они параллельны; 3. они направлены в одну сторону. Иными словами, равные векторы получаются один из другого параллельным переносом в пространстве. Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых, и компланарными, если они лежат на одной или на параллельных плоскостях. Вектор, длина которого равна единице, называется единичным вектором или ортом. Орт обозначатся 6.Способы задания векторов.1 сп.) Задание векторов координатами.О.1.Координатами в ДПСК принято называть проекцией вектора на соотв. координатные оси. Напр: Линейные операции над векторами. Сложение вектора производится по правилу параллелограмма: векторы
Это правило распространяется на любое число слагаемых: если векторы
В частности, если ломаная замыкается, т.е. Сложение векторов подчиняется обычным законам сложения ‑ сочетательному и переместительному, а также обладает обратной операцией – вычитанием. Разностью двух векторов
Векторы можно не только складывать и вычитать, но и умножать на числа (скаляры). Вектор Произведение вектора на скаляр обладает следующими свойствами: |
|||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 243. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  одинакового размера называется матрица
одинакового размера называется матрица  того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.  .
. .
.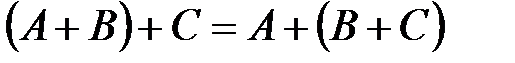 .
.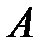 и
и  одинакового размера существует единственная матрица
одинакового размера существует единственная матрица  такая, что
такая, что 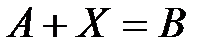 . Матрица
. Матрица 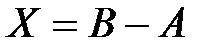 и называется разностью матриц
и называется разностью матриц  имеет решение
имеет решение  , получающаяся при этом матрица называется противоположной
, получающаяся при этом матрица называется противоположной  .
. называется матрица, все элементы которой равны соответствующим элементам матрицы
называется матрица, все элементы которой равны соответствующим элементам матрицы  .
. ;
;  ;
;  ;
;  (ассоциативность);
(ассоциативность);  (дистрибутивность);
(дистрибутивность);  (дистрибутивность).
(дистрибутивность). называется согласованной с матрицей
называется согласованной с матрицей  , если число столбцов матрицы
, если число столбцов матрицы  на матрицу
на матрицу 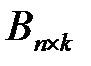 называется матрица
называется матрица  , где
, где 
 , т.е. элемент, стоящий в
, т.е. элемент, стоящий в  -той строке и
-той строке и  -том столбце матрицы произведения равен сумме произведений элементов
-том столбце матрицы произведения равен сумме произведений элементов  -го столбца матрицы
-го столбца матрицы  .
. , то
, то 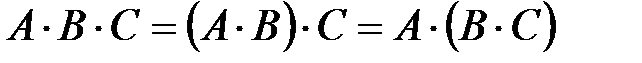 ‑ ассоциативность умножения;
‑ ассоциативность умножения; ‑ свойство дистрибутивности;
‑ свойство дистрибутивности;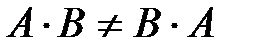 .
. - квадратная матрица порядка
- квадратная матрица порядка 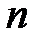 . Матрица
. Матрица  называется обратной матицей к матрице
называется обратной матицей к матрице 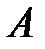 , если выполняются равенства
, если выполняются равенства  , где
, где  ‑ единичная матрица порядка
‑ единичная матрица порядка  и
и  ‑ матрицы, обратные к матрице
‑ матрицы, обратные к матрице  . Тогда
. Тогда  , с другой стороны,
, с другой стороны,  .Откуда
.Откуда  . Обратную матрицу к матрице
. Обратную матрицу к матрице  обозначают
обозначают  . Теорема 2. Матрица
. Теорема 2. Матрица  .Пусть
.Пусть  имеет обратную матрицу. Тогда
имеет обратную матрицу. Тогда  и, применяя теорему об умножении определителей, получаем
и, применяя теорему об умножении определителей, получаем  или
или  . Следовательно,
. Следовательно,  .Пусть
.Пусть  через элементы матрицы
через элементы матрицы  , а именно: если
, а именно: если  , то:
, то: ,
,
 ‑ алгебраическое дополнение к элементу
‑ алгебраическое дополнение к элементу  . Матрица получается из матрицы
. Матрица получается из матрицы  следующим образом. Сначала вместо каждого элемента
следующим образом. Сначала вместо каждого элемента  пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную
пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную  .Непосредственное умножение
.Непосредственное умножение  на матрицу слева и справа дает единичную матрицу, что подтверждает, матрица, обратная к
на матрицу слева и справа дает единичную матрицу, что подтверждает, матрица, обратная к 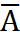 .Для того чтобы установить совместность системы нужно:1)найти ранг матрицы основной(r(A));2)найти r(
.Для того чтобы установить совместность системы нужно:1)найти ранг матрицы основной(r(A));2)найти r(  , или двумя буквами со стрелкой
, или двумя буквами со стрелкой  , где точка
, где точка  ‑ его конец.
‑ его конец. или
или  и равна длине любого его представителя, т.е. расстоянию между начальной и конечной точками связного вектора
и равна длине любого его представителя, т.е. расстоянию между начальной и конечной точками связного вектора  . Вектор, длина которого равна нулю, называется нуль-вектором и обозначается
. Вектор, длина которого равна нулю, называется нуль-вектором и обозначается  .
. .
. = (2;3) - на плоскости;
= (2;3) - на плоскости; 
 и
и  сносятся в общую точку
сносятся в общую точку  , на них строят параллелограмм
, на них строят параллелограмм  и его диагональ
и его диагональ  называют суммой векторов
называют суммой векторов 



 равен
равен  , то можно дать другое правило нахождения суммы
, то можно дать другое правило нахождения суммы  (правило треугольника): суммой векторов
(правило треугольника): суммой векторов  .
.
 образуют ломаную
образуют ломаную  , то суммой этих векторов является вектор
, то суммой этих векторов является вектор  , замыкающий эту ломаную, т.е.:
, замыкающий эту ломаную, т.е.:
 , то сумма ее звеньев равна нуль-вектору
, то сумма ее звеньев равна нуль-вектору  .
. является вектор, направленный из конца вычитаемого вектора
является вектор, направленный из конца вычитаемого вектора 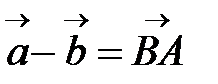 (Рис. 4.2.). Это правило следует из формулы (1): т.к.
(Рис. 4.2.). Это правило следует из формулы (1): т.к.  , то
, то  .
.
 , где
, где 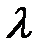 ‑ некоторое число, если:
‑ некоторое число, если: 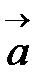 ;длина вектора
;длина вектора  раз, т.е.
раз, т.е.  ,при
,при 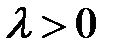 ,
,  ‑ в разные.
‑ в разные.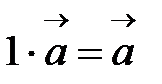 ;
; 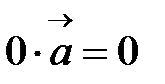 ;
;  ;
;  ;
;  .
.