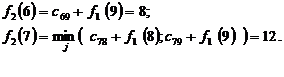Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычислительная схема динамического программирования⇐ ПредыдущаяСтр 19 из 19 Оптимальное решение задачи методом динамического программирования находится на основе функционального уравнения (1). Чтобы определить его, необходимо: 1) записать функциональное уравнение для последнего состояния процесса (ему соответствует l = n −1):
2) найти R n(S n- 1,Un) из дискретного набора его значений при некоторых фиксированных Sn−1 и Un из соответствующих допустимых областей (так как f 0 (S n ) = 0, то 3) уменьшить значение l на единицу и записать соответствующее функциональное уравнение. При l = n − k (k = 2,n) оно имеет вид
4) найти условно-оптимальное решение на основе выражения (2); 5) проверить, чему равно значение l. Если l = 0 , расчет условно-оптимальных решений закончен, при этом найдено оптимальное решение задачи для первого состояния процесса. Если l ≠ 0 , перейти к выполнению п. 3; 6) вычислить оптимальное решение задачи для каждого последующего шага процесса, двигаясь от конца расчетов к началу. Пример.Требуется перевезти груз из города А в город В. Сеть дорог, связывающих эти города, изображена на рис. 1. Стоимость перевозки груза из города s ( s =1, 9) в город j ( j = 2,10) проставлена над соответствующими дугами сети. Необходимо найти маршрут, связывающий города А и В, для которого суммарные затраты на перевозку груза были бы наименьшими. Рис.7.1
РешениеНа рис. 7.1 вершинам сети поставлены в соответствие города, а дугам — транспортные магистрали. Разобьем все множество вершин (городов) на подмножества. В первое подмножество включим исходную вершину 1, во второе — вершины, в которые входят дуги, выходящие из вершины 1, в третье — вершины, в которые входят дуги, выходящие из вершин второго подмножества. Таким образом, продолжая разбиение, получаем пять подмножеств: {1}, {2, 3, 4}, {5, 6, 7}, {8, 9}, {10}. Очевидно, что любой маршрут из города 1 в город 10 содержит ровно четыре дуги, каждая из которых связывает вершины, принадлежащие соответствующим подмножествам. Следовательно, процесс решения задачи (нахождения оптимального маршрута) разбивается на четыре этапа. На первом этапе принимается решение, через какой город, принадлежащий второму подмножеству, везти груз из города 1. На втором этапе необходимо определить, через какой город третьего подмножества везти груз из некоторого города, принадлежащего второму подмножеству, и т. д.  Перенумеруем этапы от конечной вершины сети к начальной (см. рис. 1) и введем обозначения: n — номер шага (n = 1,2,3,4); fn (s) — минимальные затраты на перевозку груза от города s до конечного города, если до конечного города осталось п шагов; jn(s) — номер города, через который нужно ехать из города s, чтобы достичь fn (s); csj — стоимость перевозки груза из города s в город j. Здесь все обозначения несут важную смысловую нагрузку: f означает целевую функцию, s — состояние системы (номер города), индекс п несет динамическую информацию о том, что из города s до конечного города осталось п шагов. Предположим, что груз доставлен в город 10, следовательно, число оставшихся шагов равно нулю (n = 0) и f n (s) = f0 (10)= 0, так как из города 10 груз везти не надо. Рассмотрим последний шаг (п = 1) и вычислим для него значение функции. Очевидно, что в город 10 груз может быть доставлен или из города 8, или из города 9. Вычислим затраты на перевозку для этих двух состояний:
Чтобы произвести расчет для п = 2, выдвинем гипотезы о месте нахождения груза: 1-я гипотеза — груз находится в городе 5; 2-я гипотеза — груз находится в городе 6; 3-я гипотеза — груз находится в городе 7. Из города 5 в город 10 можно провезти груз или через город 8, или через город 9. Поэтому оптимальный маршрут из города 5 найдется из выражения
Здесь s = 5 и j2(5) =9, т.е. условно-оптимальный маршрут проходит через город 9. Аналогично находим значения функции для s = 6 и s = 7:
Все вычисления удобно выполнять в таблицах. Расчеты первого (n =1, csj + f0 (j)) и второго (n =2, csj + f1 (j)) этапов помещены в табл. 7.1 и 7.2 соответственно. Таблица 7.1
Таблица 7.2 |
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 369. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
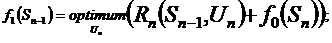
 В результате после первого шага известно решение Un и соответствующее значение функции f 1 (S n-1);
В результате после первого шага известно решение Un и соответствующее значение функции f 1 (S n-1); (2)
(2)