
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классическое, статистическое и геометрическое определения вероятностейВероятность - это количественная мера возможности появления случайного события А и обозначается она Р(А). Классическое определение вероятности.События, составляющие при данном испытании полную группу попарно несовместных, равновозможных событий, называют элементарными случаями. Те из элементарных случаев, при которых наступает событие А, называют благоприятствующими событию А. Вероятностью события А называют отношение числа благоприятствующих элементарных случаев к общему числу всех элементарных случаев. Вероятность определяется формулой где m – число элементарных случаев, благоприятствующих событию А, Пусть проводится опыт, в результате которого могут наступить те или иные события. Если эти события образуют полную группу попарно несовместных и равновозможных событий, то говорят, что опыт обладает симметрией возможных исходов и сводится к "схеме случаев". Для опытов, которые сводятся к схеме случаев, применима классическая формула вероятности. Пример 1.13. В лотерее разыгрывается 1000 билетов, среди которых 5 выигрышных. Определить вероятность того, что при покупке одного билета будет получен выигрыш. 4Элементарным событием этого опыта является покупка билета. Каждый билет лотереи неповторим, так как имеет свой номер, и купленный билет не возвращается обратно. Событие А заключается в том, что куплен выигрышный билет. При покупке одного из 1000 билетов всевозможных исходов опыта будет  Для непосредственного подсчета вероятностей удобно применять формулы комбинаторики. Рассмотрим это на примере задачи выборочного контроля. Пример 1.14. Пусть имеется партия из 4 Число всех элементарных случаев Например, пусть
Классическое определение вероятностей применимо только в тех случаях, когда испытания обладают симметрией, можно выделить равновозможные элементарные случаи и число их конечно. Для большинства реальных задач эти требования практически невыполнимы и на ряду с классическим пользуются другими определениями вероятностей. Статистическое определение вероятности. Пусть эксперимент заключается в проведении серии п испытаний, повторяющих один и тот же опыт, исходом которого может быть появление или не появление события А. И пусть во всей этой серии событие А наступило ровно Относительной частотой W(A) появления события А называют отношение числа m опытов, в которых событие А наступило, к общему числу п всех проведенных опытов: Относительная частота обладает свойством устойчивости: если число опытов в серии достаточно велико, то относительные частоты события А в различных сериях одного и того же эксперимента мало отличаются друг от друга. Статистической вероятностью события называют число, к которому стремятся относительные частоты, если число опытов неограниченно возрастает: Пример 1.15. Метеорологические наблюдения в течении 10 лет в некоторой местности показали, что число дождливых дней в июле было в разные года равно: 2; 4; 3; 2; 4; 3; 2; 3; 5; 3. Определить вероятность того, что какой-либо определенный день июля будет дождливым. 4Событие А заключается в том, что определенный день июля, например, 10 июля, пойдет дождь. Выданная статистика не содержит информации о том, в какие конкретно дни июля шел дождь, поэтому можно считать, что все дни равновозможные для этого события. Один год – это одна серия испытаний из 31 одного дня. Всего серий 10. Относительные частоты серий равны: W(A)= Геометрическое определение вероятности. Это определение вероятности обобщает классическое определение на случай, когда число элементарных случаев бесконечно. Геометрической вероятностью события А называется отношение меры Если области представляют собой а) длины отрезков
Пример 1.16. Рекламные объявления развешены с интервалом в 10 метров вдоль торгового ряда. Широта обзора у некоторого покупателя составляет 3 метра. Какова вероятность того, что он не заметит рекламу, если он движется перпендикулярно торговому ряду и пересечь ряд может в любой точке?
Задачи 1.41. Лотерея выпущена на общую сумму n гривен. Цена одного билета r гривен. Ценные выигрыши падают на m билетов. Определить вероятность выигрыша на один билет. Ответ: ( mr)/n. 1.42. 1 сентября на одном из учебных потоков экономического факультета по расписанию должно быть три занятия по разным предметам. Всего на потоке в этом семестре изучается 10 предметов. Студент, не успевший ознакомиться с расписанием, пытается его угадать. Какова вероятность успеха этого опыта, если считать, что любое расписание из трех предметов равновероятно? Ответ: 1/720. 1.43. На складе торговой фирмы находятся однотипные товары, изготовленные разными фирмами; из них: а товаров изготовлены фирмой "АВС", b товаров – фирмой "F&N", с товаров – фирмой "ЭХО". При ревизии на складе просматривают один за другим все имеющиеся товары и отмечают места их изготовления. Найти вероятность того, что при этом: а) первым появится товар фирмы "F&N"; б) из m просмотренных товаров k (k£c) будут фирмы "ЭХО"; в) из m просмотренных товаров все m (m£b) будут фирмы "АВС". Ответ: а) b/(a+b+c); б ) 1.44. На книжной полке в случайном порядке расставлено 20книг, среди них двухтомник Л.Н. Толстого "Война и мир". Предполагая, что различные расположения книг равновероятны, найти вероятность того, что оба тома будут расположены рядом. Ответ . 0,1. 1.45. На круглой вращающейся полке расставлено 10 видеокассет, среди них два видеофильма с Р. Гиром в главной роли. Предполагая, что различные расположения кассет равновероятны, найти вероятность того, что оба фильма с Р. Гиром будут стоять рядом. Ответ: 2/9 . 1.46. В коробке лежит 20 канцелярских кнопок, из них 5 – бракованных. Наугад взяли 10 кнопок. Найти вероятность того, что среди них: а) нет бракованных; б) ровно одна бракованная; в) ровно две бракованные. Ответ: а) 0,0162; б) 0,135; в) 0,348. 1.47. Найти вероятность того, что дни рождения 12 человек придутся на различные месяцы года. Ответ: 12!/ 12 1.48. Из колоды в 36 карт вынуты три карты. Какова вероятность того, что: 1) две из них бубновой масти; 2) две из них одной масти; 3) хотя бы одна из них бубновой масти; 4) хотя бы одна из них ‑ туз? Ответ: а) 0,136; б) 0,545; в) 0,5903; г) 0,305. 1.49. В урне имеются 10 шаров: 3 белых, 2 красных и 5 черных. Из урны наугад вынимается один шар. Найти вероятность того, что этот шар: а) белый; б) черный; в) не белый, г) белый или красный; д) не черный. Ответ: а) 0,3; б) 0,5; в) 0,7; г) 0,5; д) 0,5. 1.50. Брошены три монеты. Найти вероятность, что выпадут а) два герба; б) три герба; в) герб не выпадет. Ответ: а) 3/8; б) 1/8; в) 1/8. 1.51. Игральная кость бросается один раз. Какова вероятность того, что выпадет: а) четное число очков; б) 4 очка; в) не более 3 очков. Ответ: а) 0,5; б) 1/6. в) 1/2. 1.52. В урне 3 белых и 7 черных шаров. Наудачу извлекли 2 шара. Какова вероятность того, что они будут разного цвета? Ответ: 7/15. 1.53. Какова вероятность того, что в выбранном наугад трехзначном номере две цифры одинаковые, а третья отличается от них? Ответ: 0,27. 1.54. Полная колода карт (52 карты) делится случайным образом на две равные части. Найти вероятности того, что: а) в каждой части окажется по два туза; б) в одной из частей не будет ни одного туза; в) в одной из частей будет ровно один туз. Ответ: 1.55. Карточка лотереи содержит 49 номеров. Для участия в лотерее необходимо купить карточку, отметить в ней 6 номеров и карточку сдать. При розыгрыше тиража лотереи определяется 6 выигравших номеров из 49. Найти вероятности событий: Аi={верно угаданы i выигрышных номера из 6}, если i =3,4,5,6. Ответ: 1.56. В картотеке 20 перенумерованных карточек. Наугад вынимают одну за другой и номера записывают. Какова вероятность того, что номера будут идти: а) в естественном порядке: 1,2,…,20; б) в обратном порядке: 20,19,…,1. Ответ: а) 1/20!; б) 1/20!. 1.57. Решить предыдущую задачу при условии, что каждая карточка после вынимания и записи номера кладется обратно и перемешивается с остальными. Ответ: 1/20 1.58. В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований имеется 5 команд экстракласса. Найти вероятность того, что: а) все команды экстракласса попадут в одну группу; б) две команды экстракласса попадут в одну группу, а три – в другую. Ответ: а) 1/68; б) 6/17. 1.59. Окрашенный куб распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: а) одну; б) две; в) три; г) ни одной окрашенной грани. Ответ: а) 0,384; б) 0,096; в) 0,008; г) 0,512. 1.60. Какова вероятность соединиться с нужным абонентом, набрав наугад шестизначный телефонный номер, состоящий из различных цифр? Как изменится эта вероятность, если а) наугад набраны только три забытые цифры; б) если цифры номера могут повторяться? Ответ: 1.61. Из четырех букв разрезной азбуки составлено слово "соль". Ребенок, не умеющий читать, рассыпал эти буквы и собрал в произвольном порядке. Найти вероятность того, что у него получится слово "лось". Ответ: 1/24.. 1.62. В условиях предыдущей задачи, какова вероятность того, что из рассыпавшегося слова "колокол" будет составлено опять слово "колокол"? Ответ: 1/210. 1.63. Ребенок, играя шестью карточками, на которых написаны буквы: М,Л,К,О,О,О, сложил слово "МОЛОКО". Какова вероятность того, что он не умеет читать? Какой будет вероятность этого события, если ребенок играет десятью карточками с буквами: М,М,Т,Т,А,А,А,К,И,Е, и складывает слово "МАТЕМАТИКА"? Ответ: 1/120; 2!2!3!/10!=24/10!. 1.64. В кондитерской имеется 7 видов пирожных. Покупатель выбил чек на 4 пирожных. Считая, что любой набор пирожных равновероятен, вычислить вероятность того, что покупатель заказал: а) пирожные одного вида; б) пирожные разных видов; в) по два пирожных различных видов. Ответ: 1.65. Для участия в телепередачи об университете необходимо выбрать 5 студентов. Студенты выбираются случайным образом из победителей студенческих олимпиад, которых в университете 15 человек, среди них 4 – студенты первого и второго курсов, 6 третьекурсников и 5 старшекурсников. Найти вероятности того, что: а) будут выбраны одни третьекурсники; б) все первокурсники и второкурсники будут участвовать в передаче; в) в передаче будут участвовать только старшекурсники; г) ни один третьекурсник не попадет на передачу; д) будут выбраны: два студента младших курсов, один студент третьего курса, 2 студента старших курсов. Ответ: а) 0,002; б) 0,0036; в) 0,0003; г) 0,042; д) 0,12. 1.66. Какова вероятность того, что в группе из 30 студентов у двоих дни рождения совпадут? Ответ: 1.67. В доме 7 этажей. На первом в лифт входят 3 человека. Каждый из них с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Найти вероятность того, что 1) все выйдут на четвертом этаже; 2) все выйдут одновременно на любом из этажей. Ответ: а) 1/216; б)1/36. 1.68. В группе 30 человек, из которых 6 отличников. Группа случайным образом разбита на две равные подгруппы. Какова вероятность того, что в каждой подгруппе по три отличника? Ответ: 0,349. 1.69. При испытании партии приборов относительная частота годных приборов оказалась равной 0.9. Найти число годных приборов, если всего было проверено 200 приборов. Ответ: 180. 1.70. При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов? Ответ: п = 30. 1.71. Отдел технического контроля обнаружил 6 бракованных деталей в партии из случайно отобранных 60 деталей. Найти относительную частоту появления брака. Ответ: 0,1. 1.72. Двое студентов договорились встретиться в интервале времени от 9.00 до 10.00. Каждый пришедший ожидает встречи 15 минут, затем уходит. Какова вероятность того, что встреча произойдет? Ответ: 7/16. Указание: Обозначить время прихода одного студента х, второго у и рассмотреть геометрическую вероятность выполнения неравенства 1.73. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода – один час, а второго – два часа. Ответ: 0,12. 1.74. Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна 10мм, а расстояние между их осями равно 100мм? Ответ: ≈ 0,19. 1.75. В шкафу находятся 10 пар ботинок различных сортов. Из них случайно выбирают 4 ботинка. Найти вероятность того, что среди выбранных ботинок отсутствуют парные. Ответ: 1.76. Среди 25 экзаменационных билетов 5 «легких». Два студента берут по очереди по одному билету. Найти вероятности событий: а) первый студент взял «легкий» билет; б) второй студент взял «легкий» билет; в) оба студента взяли «легкие» билеты. Ответ: а) 0,2; б) 0,2; в) 0,0333. 1.77. На шахматную доску из 64 клеток наудачу ставятся две ладьи белого и черного цвета. С какой вероятностью они будут бить друг друга? Ответ: 2/9. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 505. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1.7)
, (1.7)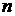 ‑ число всех возможных элементарных случаев.
‑ число всех возможных элементарных случаев.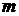 =5. Вероятность получить выигрыш, купив один билет, равна Р(А) =
=5. Вероятность получить выигрыш, купив один билет, равна Р(А) =  = 0.005.3
= 0.005.3 изделий, среди них есть
изделий, среди них есть 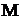 бракованных. Для контроля отбирается часть из
бракованных. Для контроля отбирается часть из 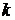 изделий. Какова вероятность того, что среди отобранных изделий будет ровно
изделий. Какова вероятность того, что среди отобранных изделий будет ровно 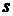 бракованных?
бракованных?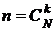 . Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет
. Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет 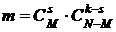 . Тогда искомая вероятность
. Тогда искомая вероятность  .
. =
=  =
=  =
=  » 0.408. 3
» 0.408. 3 . (1.8)
. (1.8) . (1.9)
. (1.9)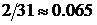 ,
,  ,
,  ,
,  ,
,  ,
, 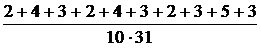 =
=  .3
.3 области, благоприятствующей появлению события, к мере
области, благоприятствующей появлению события, к мере  всей области:
всей области: 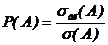 (1.10)
(1.10) , б) площади фигур
, б) площади фигур 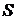 , в) объемы пространственных фигур
, в) объемы пространственных фигур  , то геометрические вероятности соответственно равны:
, то геометрические вероятности соответственно равны: ;
;  ;
;  . (1.11)
. (1.11) 4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р =
4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р = 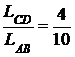 =0.4. 3
=0.4. 3 ; в)
; в)  .
. .
.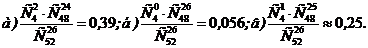


 .
.

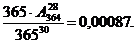
 в квадрате со сторонами
в квадрате со сторонами  .
.