
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прямозубые конические колеса. Геометрические параметры. Силы действующие в прямозубой передаче.Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом Σ. Наиболее распространены передачи с углом Σ = 90°.
Силы:
В зацеплении К.П. действуют силы: окружная Ft, радиальная Fr и осевая Fa. По нормали к зубу действует сила Fn. Которая раскладывается на Ft и Fr’. В свою очередь Ft’ раскладывается на Fa и Fr. · Ft=2T1/dm1, Fn=Ft/cos α, · Fr’=Ft tg α · Fr=Fr’ cos δ1=Ft tg α sin δ1, · Fa=Ft’ sin δ1=Ft tg α sin δ1 Для колеса направление сил противоположно. При этом Fa является радиальной силой , а Fr- осевой.
Прямозубое цилиндрическое колесо эквивалентное коническому. Расчет зубьев прямозубых конических передач на прочность по контактным напряжения изгиба. Эквивалентным называется такое воображаемое прямозубое цилиндрическое колесо, размеры и форма зуба которого соответственно совпадают с размерами и формой зуба реального конического колеса в его сечении средним дополнительным конусом.
bv=b uv=dv2/dv1=dm2cos δ1/cos δ2dm1 поскольку при d1 + d2 = 90° cos d1 = sin d2 un = u* tg d2 = u^2 Для проверочного расчета прямозубых конических передач: σH=1.18 где vH = 0.85- опытный коэффициент Для проектного расчета формулу преобразуют, при этом учитывают, что основными габаритными размерами для конических передач является dl2 и Rp1 нагрузки характеризуются моментом T2 на ведомом валу. После преобразования получают: dl2=1.7*  Определение допускаемых напряжений в зубчатых передачах при постоянном режиме нагружении для случаев, когда действительное число циклов нагружения больше или меньше базового. При постоянном режиме нагрузки расчетное число циклов перемены напряжений: NH=60 nct Где n – частота вращения того из колес, по материалу которого определяют допускаемые напряжения, об/мин; с- число зацеплений зуба за один оборот колеса (c равно числу колес, находящихся в зацеплении с рассчитываемым); t- число часов работы передачи за расчетный срок службы. Отметим, что в большинстве случаев практики NH>NH0. Этот режим нагрузки является наиболее тяжелым для передачи. Его принимают за расчетный так же для неопределенных режимов нагрузки. Допускаемое контактное напряжение [sН] прямо пропорционально твердости поверхности материала детали. [sН]= sн0/Sн*КнL
I)
II) NHG < NHi KHL ≤ 1 sНi= sн0*КнL при напряжении равном sН 0 передача может работать практически бесконечно долго, брать в расчет напряжение sН i < sН 0 не имеет смысла. В связи с этим принимают коэффициент KHL = 1. Таким образом, окончательно можем записать 1 <= KHL<=2.4. .
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 451. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 dm – средний делительный диаметр. de – внешний делительный диаметр. Rm – среднее конусное расстояние. Re – внешнее конусное расстояние. b – ширина зубчатого венца. δ- углы делительных конусов
dm – средний делительный диаметр. de – внешний делительный диаметр. Rm – среднее конусное расстояние. Re – внешнее конусное расстояние. b – ширина зубчатого венца. δ- углы делительных конусов 

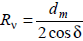 dv1= dm1/cos δ1
dv1= dm1/cos δ1
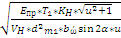 ≤[σH]
≤[σH] где Kbl=bώ/R1- коэффициент ширины зубчатого венца .
где Kbl=bώ/R1- коэффициент ширины зубчатого венца .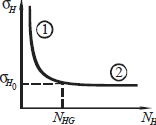
 Кривя усталости
Кривя усталости где m-степенной показатель функц
где m-степенной показатель функц
 NHG > NHi, то KHL > 1,
NHG > NHi, то KHL > 1, где NHi = 60niLi – действительное число циклов нагружения при воздействии напряжения sН i ; Li – число часов работы при действии напряжения sН i.
где NHi = 60niLi – действительное число циклов нагружения при воздействии напряжения sН i ; Li – число часов работы при действии напряжения sН i.  эквивалентного числа циклов нагружения
эквивалентного числа циклов нагружения