
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет зубьев и прямозубых цилиндрических колес на изгиб. Вывод формул для проверочного проектного расчета.Наибольшие напряжения изгиба возникают у основания зуба в зоне перехода эвольвентной поверхности в галтель. Здесь же наблюдается концентрация напряжений. Допущения: 1. в зацеплении находится одна пара зубьев; 2. сила приложена к вершине зуба; 3. силами трения на поверхности зуба пренебрегаем; 4. радиальной силой Fr в расчете пренебрегаем 5. зуб рассматриваем как консольно закрепленную балку, для которой справедлива гипотеза плоских сечений.
Напряжения изгиба в опасном сечении, расположенном вблизи хорды основной окружности db
b – ширина зубчатого венца, s – толщина основания зуба в опасном сечении, l – расстояние от опасного сечения до места приложения нагрузки Расчет зубьев на изгиб проводят по условию
KT – теоретический коэффициент концентрации нагрузки KF – коэффициент расчетной нагрузки
действительные напряжения изгиба в опасном сечении
безразмерные коэффициенты:
где YF – коэффициент формы зуба
Проектный расчет выразим окружную силу Ft через мощность P
коэффициент ширины зуба
Условие равной прочности зубьев колес и шестерни по напряжениям изгиба. Условие равной прочности по напряжению изгиба m≥267 Известно, что в условиях равной прочности геометрические размеры должны быть одинаковыми, m1=m2; P1=P2; KF1=KF2; z1n1»z2n2; YF 1/[σF]1= YF 2/[σF]2 - условие, обеспечивающее равную прочность Тот из зубьев у которого отношение YF/[sF] больше и есть менее прочный по напряжению изгиба. его и следует взять за основу при расчете m YF – коэффициент формы зуба; z- количество зубьев; m- модуль; KF – коэффициент расчетной нагрузки; 
Косозубые цилиндрические колеса. Геометрические параметры. Силы действующие в косозубой передаче. У косозубых колес зубья расположены не по образующей делительного цилиндра, а составляют с ней угол β Профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба. Модуль в этом сечении должен быть так же стандартным. В торцевом сечении t-t или окружном направлении параметры косового зуба изменяются в зависимости от угла β: · Окружной шаг pt=pn/cos β, Окружной модуль mt=mn/cos β, Диаметр делительной окружности d=mtz=mnz/cos β.
Силы действующие в косозубых передачах:
Здесь силу Fn раскладывают на три составляющие: · Окружную силу Ft=2T/d · Осевую силу Fa=Ft tg β · Радиальную силу · Нормальная сила В косозубом цилиндрическом колесе линия контакта расположена наклонно, а нагрузка по линии контакта распределяется неравномерно. Наибольшая нагрузка наблюдается при зацеплении зубьев в средней части линии контакта в связи с тем, что в этом случае суммарная жесткость взаимодействующих зубьев наибольшая. Прямозубое цилиндрическое колесо, эквивалентное косозубому. Вывод формулы для эквивалентного диаметра и числа зубьев. Расчет косозубой передачи на прочность по контактным напряжениям и по напряжениям изгиба. Эквивалентным называется такое воображаемое прямозубое цилиндрическое колесо, форма и размеры зуба которого соответственно совпадают с формой и размерами зуба реального косозубого колеса в его нормальном сечении. Нормальное сечение n–n косозубого колеса имеет форму эллипса с полуосями a и b'
Радиус кривизны эллипса
диаметр эквивалентного колеса
число зубьев
По контактным напряжениям Коэффициент повышения прочности
значения ZНb в формуле предварительно оценивают приближенно; при некоторых средних значениях: b = 12°; ea = 1,5; KHa = 1,1, получим ZНb = 0,85.
По напряжениям изгиба.
прочности по напряжению изгиба
при b > 40° принимают Yb = 0,7; Ea – коэффициент торцевого перекрытия, учитывает уменьшение нагрузки ввиду многопарности зацепления
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 530. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


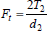

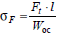
 осевой момент сопротивлен
осевой момент сопротивлен 



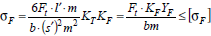
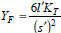
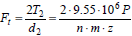






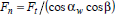



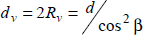
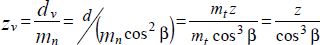
 KHa – коэффициент учитывающий неравномерность распределения нагрузки ea – коэффициент торцевого перекрытия
KHa – коэффициент учитывающий неравномерность распределения нагрузки ea – коэффициент торцевого перекрытия

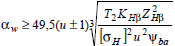 или
или
 YF – коэффициент формы зуба KF = KFβ*KFν – коэффициент расчетной нагрузки; b – ширина колеса; mn – модуль в нормальном сечении; ZFb – коэффициент повышения
YF – коэффициент формы зуба KF = KFβ*KFν – коэффициент расчетной нагрузки; b – ширина колеса; mn – модуль в нормальном сечении; ZFb – коэффициент повышения Yb – коэффициент учитывающий повышение изгибной прочности
Yb – коэффициент учитывающий повышение изгибной прочности
