Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистические характеристики распределений порога значимости по данным Fitch, (тыс. долларов США)⇐ ПредыдущаяСтр 16 из 16
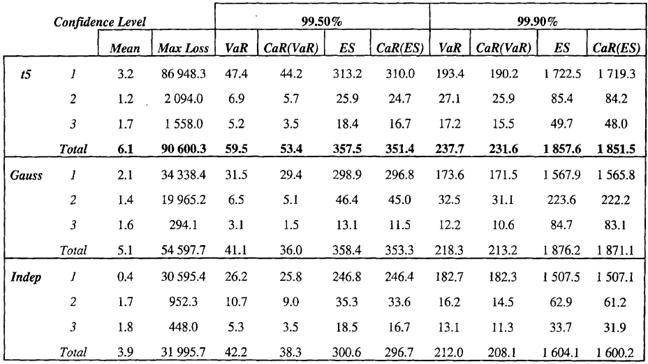
Приложение 4 «Оценка вероятностных распределений убытков» Таблица 4.1
Таблица 4.2
Продолжение приложения 4
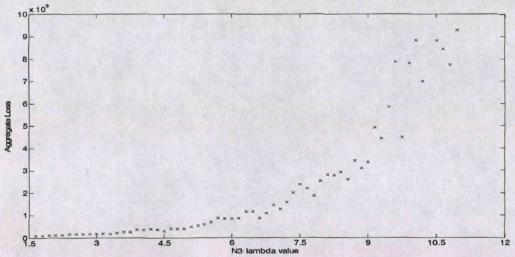
Рис.4.1
Приложение 5 «Стохастическое моделирование величины совокупного убытка»
Рис.5.1
Рис.5.2
Рис.5.3 Приложение 6 «Сравнение расчетных значений рискового капитала»
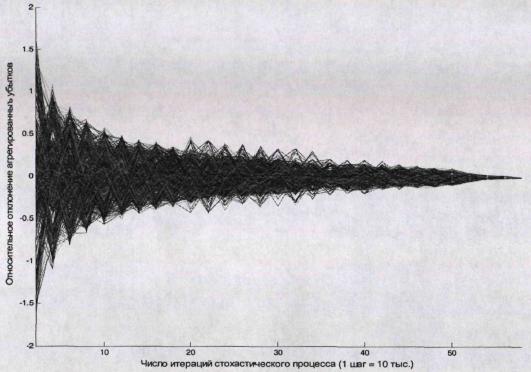
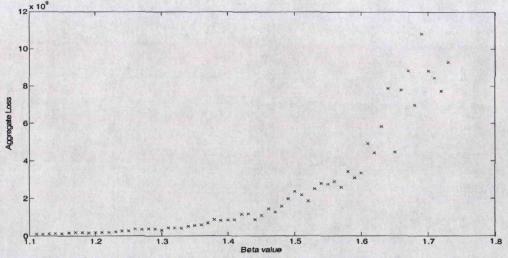
Приложение 7 «Анализ сходимости и устойчивости модели»
Рис.7.1
Рис.7.2
Продолжение приложения 7 Рис.7.3
Приложение 8 «Листинг MATLAB» function Freq_Sim_Mtrx = Frequency_Pois_Generation(lambda, Corr_Matrix, sim_count) busines_lines = 3; %столбцы 1-3: Independent Pois(lambda(i)) %столбцы 4-6: Perfect Dependency Pois(lambda(i)), normal copula,1 Correlation Mtrx %столбцы 7-9: Pois(lambda(i)), normal copula, Sigma Correlation Mtrx %столбцы 10-12: Pois(lambda(i)), tcopula(nu=1) %столбцы 13-15: Pois(lambda(i)), tcopula(nu=3) %столбцы 16-18: Pois(lambda(i)), tcopula(nu=5) %----------------------------------------Independent rnd generation for i=1:busines_lines Freq_Sim_Mtrx(:,i)=poissrnd(lambda(i),sim_count,1); end %----------------------------------------Copula's family generation Gauss_u1=copularnd('Gaussian',1,sim_count); Gauss_u2=copularnd('Gaussian',Corr_Matrix,sim_count);
Student_t1_u=copularnd('t',Corr_Matrix,1,sim_count); Student_t3_u=copularnd('t',Corr_Matrix,3,sim_count); Student_t5_u=copularnd('t',Corr_Matrix,5,sim_count); 
for i=1:busines_lines Freq_Sim_Mtrx(:,i)=poissrnd(lambda(i),sim_count,1); end
for i=(busines_lines + 1):(busines_lines*2) Freq_Sim_Mtrx(:,i)=poissinv(Gauss_u1(:,i-busines_lines),lambda(i-busines_lines)); end
for i=(busines_lines*2 + 1):(busines_lines*3) Freq_Sim_Mtrx(:,i)=poissinv(Gauss_u2(:,i-busines_lines),lambda(i-busines_lines)); end
for i=(busines_lines*3 + 1):(busines_lines*4) Freq_Sim_Mtrx(:,i)=poissinv(Student_t1_u(:,i-busines_lines*2),lambda(i-busines_lines*2)); end
for i=(busines_lines*4 + 1):(busines_lines*5) Freq_Sim_Mtrx(:,i)=poissinv(Student_t3_u(:,i-busines_lines*4),lambda(i-busines_lines*4)); Продолжение приложения 8 end
for i=(busines_lines*5 + 1):(busines_lines*6) Freq_Sim_Mtrx(:,i)=poissinv(Student_t5_u(:,i-busines_lines*6),lambda(i-busines_lines*6)); end end
function Loss = Loss_on_step_i(Freq_Sim_Mtrx,busines_lines,sim_count) %функция генерирует матрицу агрегированных убытков с заданными %распределениями по бизнес линиям, определенных в массиве busines_lines %массив Freq_Sim_Mtrx-задает частоты наступления событий для busines_lines %sim_count - задаёт число симуляций расчёта S(1:3)=0;
for i=1:length(busines_lines)
%Генерируем матрицу искомых случайных величин высотой sim_count и шириной - %кол-во убытков для busines_lines(i), %затем суммируем убытки и усредняем по всем симуляциям
switch busines_lines(i)
case 1 S(busines_lines(i))= mean(sum( gprnd(0.127,0.138,6.293,sim_count,Freq_Sim_Mtrx(busines_lines(i)))'));
case 2 S((busines_lines(i))= mean(sum( gprnd(0.778,1.054,4.581,sim_count,Freq_Sim_Mtrx(busines_lines(i)))'));
case 3 S((busines_lines(i))= mean(sum( gprnd(0.352,0.432,5.636,sim_count,Freq_Sim_Mtrx(busines_lines(i)))'));
end
end %i
Loss=S; end Продолжение приложения 8
function Loss = Agregate_Loss(Freq_Sim_Mtrx,busines_lines,sim_count) b_l = 3; len = length(Freq_Sim_Mtrx(:,1)); L(1:len,1:b_l) = 0; Loss(1:len,1:(b_l+1)) = 0; Loss_Visual(1:floor(len/100),1:(b_l+1)) = 0; for i = 1:len L(i,:)=Loss_on_step_i(Freq_Sim_Mtrx(i,1:b_l),busines_lines,sim_count); end % %-------------------------------------------------------расчет VaR и CVaR % srl = sort(sum(L(:,:)')); % сортировка (по возрастанию) величины агрегированного убытка на каждом шаге % симуляций % threshold = floor(conflvl*len); %вычисление порога CVaR % % VaR = srl(threshold); % CVaR = mean(srl(1:threshold,1)); % %--------------------------------------------------------вывод переменных Loss(:,2:(b_l+1)) = L; Loss(:,1) = sum(L'); %суммирует убытки по строкам по всем бизнес линиям
for i = 2:floor(len/100) Loss_Visual(i,:) = mean(Loss((i-1)*100:i*100,:)); end
Loss_Visual(1,:) = mean(Loss(1:100,:)) % % Loss(1,:) = mean(L); % в первую строку Loss выводим среднюю величину убытка по всем траекториям % по каждой бизнес-линии % Loss(2,1) = sum(Loss(1,:)); % в ячейке Loss(2,1) выводим суммарную величину агрегированного убытка по % всем траекториям % Loss(2,2) = VaR; % Loss(2,2) = CVaR; % ----------------------------------------------- визуализация траекторий
Продолжение приложения 8 hold on; for i = 1:length(busines_lines) plot(Loss_Visual(:,busines_lines(i)+1),'LineWidth',1,'LineStyle','-'); end
plot(Loss_Visual(:,1),'LineWidth',1.5,'Color','b','LineStyle','-');
end
function CaR = CaR_Calculation(Sim_Column,conf_lvl)
len = length(Sim_Column(:)); %--------------------------------------------------------расчет VaR и CVaR srl = sort(Sim_Column(:)'); % сортировка (по возрастанию) величины убытка threshold = floor(conf_lvl*len); % вычисление порога CVaR VaR = srl(threshold); ES = mean(srl(threshold:len)); %----------------------------------------------------------вывод переменых
CaR(1) = mean(Sim_Column(:)); % ожидаемые убытки (Expected Loss) CaR(2) = max(Sim_Column(:)); % максимальный убыток CaR(3) = VaR;
% в ячейке Loss(2,1) выводим суммарную величину агрегированного убытка по % всем траекториям CaR(4) = ES;
end
function Cnv = Convergence_Analysis(Loss)
V_Mtrx(1:1000,1:30)=0; l=length(Loss); step=3000; DV(1:30,1:999)=0;
for j = 1 : 29 % число векторов размерности 1х100
for k = 1 : 999 % поэлементное вычисление значений векторов
Продолжение приложения 8 i_rnd=ceil( (l-j*step)*rand());
% генерируем случайный индекс начала отсчёта в интервале [0,len-j*step]
V_Mtrx(k,j)=mean(Loss(i_rnd : i_rnd + j*step)); end;
Cnd=DV; hold on; plot([DV(2,:);DV(3,:);DV(4,:);DV(5,:);DV(6,:);DV(7,:);DV(8,:);DV(9,:); DV(10,:);DV(11,:);DV(12,:);DV(13,:);DV(14,:);DV(15,:);DV(16,:); DV(17,:);DV(18,:);DV(19,:);DV(20,:);DV(21,:);DV(22,:);DV(23,:); DV(24,:);DV(25,:);DV(26,:);DV(27,:);DV(28,:);DV(29,:);DV(30,:)] 'LineWidth',1,'LineStyle','-'); end
function Out = Optimal_Insurance_Fit(Loss_Mtrx,Mitigation_val,conf_lvl)
% в 1 столбце - суммарный убыток, во 2ом - 1й категории (по которой % подбираем франшизу), % 3,4 - убытки по категория 2,3 соответственно
Len = length(Loss_Mtrx(:,1)); Max_Loss = max(Loss_Mtrx(:,2)); step = 100; VaR = CaR_Calculation(Loss_Mtrx(:,2),conf_lvl); VaR_in = VaR(3); VaR_cur = VaR_in; MLoss = Max_Loss; while (VaR_cur / VaR_in)>(1-Mitigation_val) R(1) = MLoss; R(2) = VaR_cur;
MLoss = Max_Loss / step; Max_Loss_Curr(1:Len,1)=MLoss; Loss_Mtrx(:,2) = min (Loss_Mtrx(:,2), Max_Loss_Curr); VaR = CaR_Calculation(Loss_Mtrx(:,2),conf_lvl); VaR_cur = VaR(3); end Out=R; end [1] Егорова Н.Е.,Смулов А.С.Предприятия и банки: взаимодействие, экономический анализ и моделирование.-М.;Дело,2002. С.61. [2] Емельянов А.А. Имитационное моделирование в управлении рисками. -СПБ: Санкт-Петербургская инженерно-экономическая академия, 2000. С.132. [3] Емельянов А.А. Имитационное моделирование в управлении рисками. -СПБ: Санкт-Петербургская инженерно-экономическая академия, 2000. С.24 [4] Емельянов А.А. Имитационное моделирование в управлении рисками. -СПБ: Санкт-Петербургская инженерно-экономическая академия, 2000. С.58. [5] Емельянов А.А. Имитационное моделирование в управлении рисками. -СПБ: Санкт-Петербургская инженерно-экономическая академия, 2000. С.79. [6] Колемаев В.А. Математическая экономика. - М.: ЮНИТИ, 1998. С.68. [7] Артюхов СВ., Базюкина О.А., Королев В.Ю., Кудрявцев А.А. Модель оптимального ценообразования, основанная на процессах риска со случайными премиями. // Системы и средства информатики. Специальный выпуск. - М.: ИПИРАН, 2005. С.102 [8] Щелов О. Управление операционным риском в коммерческом банке. Бухгалтерия и банки, 2006 - №6. С.112 [9] Лобанов А.А., Чугунов А.В. Энциклопедия финансового риск- менеджмента. - М., Альпина Бизнес Букс, 2005. С.89. [10] Лобанов А.А., Чугунов А.В. Энциклопедия финансового риск- менеджмента. - М., Альпина Бизнес Букс, 2005. С.134. [11] Бенинг В. Е., Королев В. Ю. Введение в математическую теорию риска. - М.: МАКС-Пресс, 2000. С.194. [12] Бенинг В. Е., Королев В. Ю. Обобщенные процессы риска. — М.: МАКС-Пресс, 2000. С.173 [13] Бенинг В. Е., Королев В. Ю. Обобщенные процессы риска. — М.: МАКС-Пресс, 2000. С.15. [14] Бенинг В. Е., Королев В. Ю. Обобщенные процессы риска. — М.: МАКС-Пресс, 2000. С.25. [15] Бенинг В. Е., Королев В. Ю. Обобщенные процессы риска. — М.: МАКС-Пресс, 2000. С.71 [16] Катилова Н.В., Сорин Э. Практика ключевых индикаторов для операционных рисков. Управление финансовыми рисками - №2, 2006. С.234 [17] Сазыкин Б.В. Управление операционным риском в коммерческом банке. - М.: Вершина, 2008. С.113 [18] Дубров A.M., Лагоша Б.А., Хрусталёв Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе. - М.: Фин. и стат., 2000. С.241. [19] Королев В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска: Учебн. Пособ.- М.:ФИЗМАТЛИТ, 2007. С.198. [20] Меньшиков И.С., Шелагин Д.А. Кооперативное распределение рискового капитала. - М.: Вычислительный центр РАН, 2001.С.201 [21] Васин А.А., Морозов В.В. Теория игр и моделей математической экономики. - М.: МАКС Пресс, 2005.С.178. [22] Ауман Р., Шепли Л. Значения для неатомических игр. - М. Мир, 1997.С1.9. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 365. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


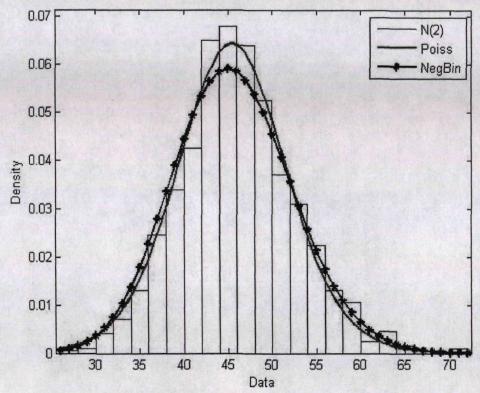
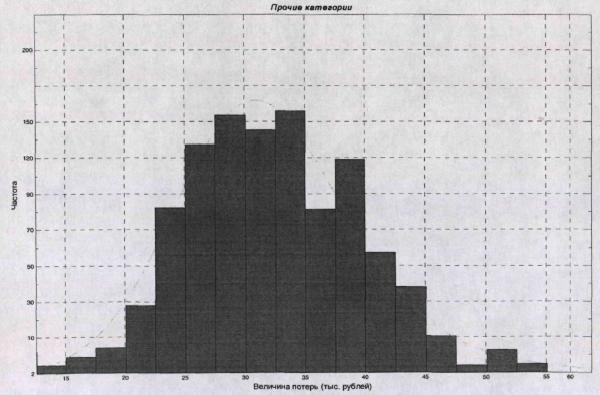 Рис.4.2
Рис.4.2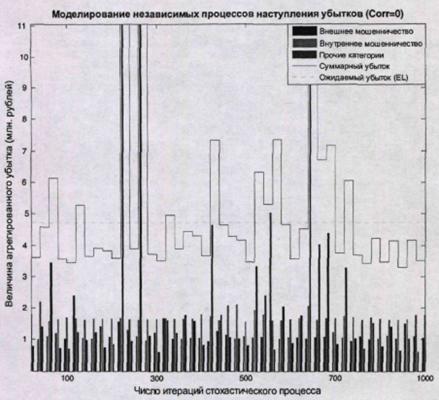
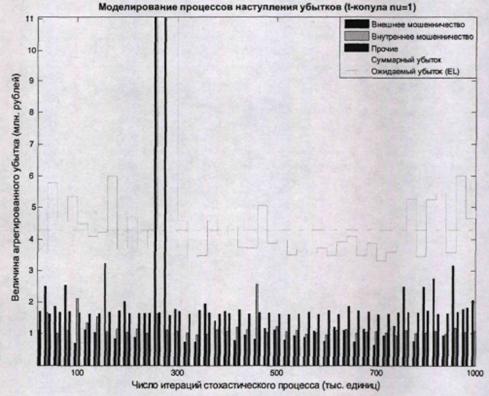
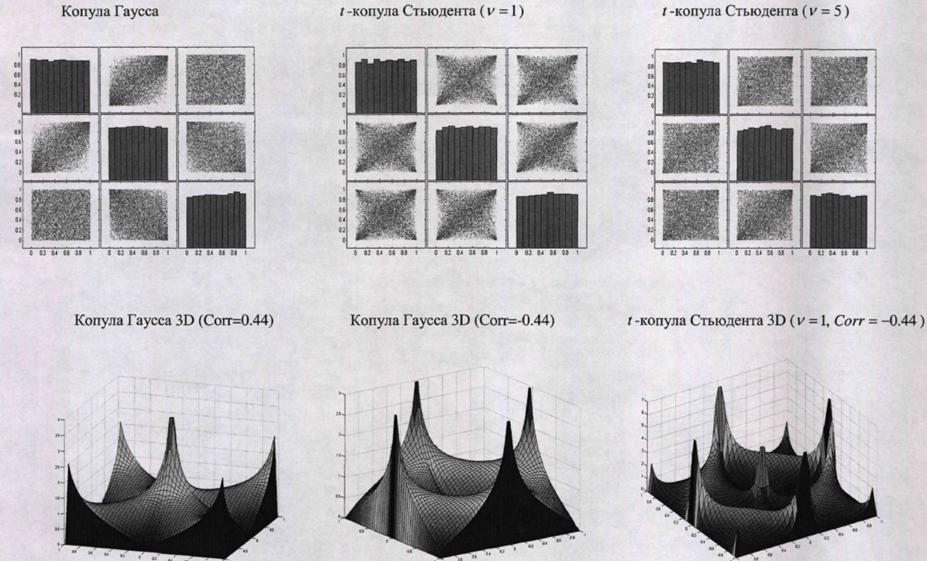 Продолжение приложения 5
Продолжение приложения 5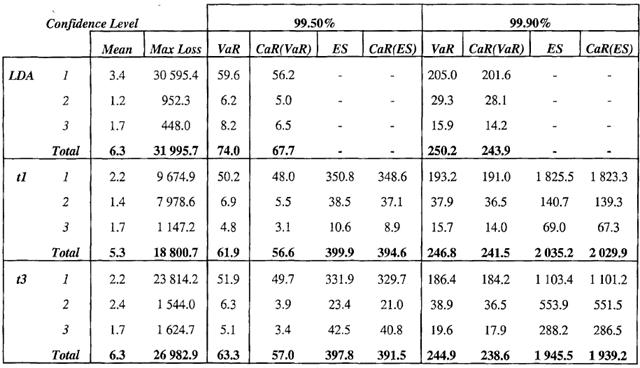 Таблица 6.1
Таблица 6.1